Survival of the Steepest

Most textbooks tell you that the evolutionary process is really quite simple: three rules are all that's necessary: inheritance, variation, and selection. It is indeed true that these three rules are all that's needed for evolution to occur, but that does not mean that the evolutionary process is simple. In fact, quite the opposite. Real systems evolve in many different ways because the process takes place (is "instantiated") in many different environments. How the evolutionary process unfolds depends very much on those environments: they shape the mode and manner of adaptation.


Let me explain what I mean in more detail. How do the three necessary elements depend on the environment? The inheritance part of the "Darwinian Triad" isn't actually that susceptible to environmental variations (although there are cases). Variation (that is, changes incurred during transmission of genetic information from parent to child), and in particular selection, are very much subject to modulation by the environment. There are likely dozens of books written about the different ways that changes can occur to the carriers of information (yes, DNA) during replication, and this post won't be the one dwelling on those details. They are important, just not for this post. Here, we'll discuss the third pike of the Triad: selection.


It is very unlikely that you are reading this without being fairly well-versed in evolutionary biology, but just in case you got here from reading about black holes, here it is in a nutshell. Evolution occurs because random changes (variation) in the genetic information (that which is inherited) change the frequency at which that information is represented in a population, simply because the information is about how to make many copies of that information. Thus, information that is not increasing the fit of the organism to its environment tends to become less-represented, while information that leads to a better fit will increase in numbers, simply because a good fit means many copies. I realize that this may not be the way you have been taught the word "fitness" in the context of evolutionary biology in class, but it should have been.


Selection, by this account, really just means that "good info will be rewarded", in the sense that good info will increase the info-carrier's number of copies in the population. And because the world in which we (and this information) lives is finite, when one type gets to have more copies, there must be fewer of the less-fit types. As a consequence we will find that, over time, fitness along with the information on how to make a fit organism, increases over time on average. Most of the time.



Only most of the time?

Well yes, this law about the increase of information in evolution is not an absolute one. For example, because the information in your genome is about the world in which you live, it follows that when the world changes then some of what used to be information is ... not ... information anymore. And because information makes you fit, your fitness will almost always drop when the world has changed for you. But there are other cases where fitness can decrease in selection, and this post is about one of them.


There is a fairly classical (by now) case where lower fitness is actually selected for, and we need to talk about it briefly because it is relatively well-known and--it turns out--is somewhat of a bookend to the case I'll introduce you to shortly. This case is called the "Survival of the Flattest" effect (this is a pun meant to remind you that due to this effect, it is not the fittest that survives). Indeed, in this particular case fitness, measured in terms of the number of copies that the information--meaning the genome--can make, can drop in evolution. This happens if the mutation rate is very high, and there are fitness peaks that are not so very high, but kind of "flat" instead, so that mutated copies of the information are mostly still informative. In order not to make this post too long, I'l refer you to the Wiki page that describes this effect, and just show the video from that Wiki link that describes the effect, below.

The authors of this video were, incidentally, a grad student (Randy Olson) and a postdoc (Bjørn Østman) from my lab at Michigan State University at the time. And the not so humblebrag disclosure is that the effect was actually discovered in my lab at Caltech in 2001. You can read all about that by googling it.


But let's get back to the matter at hand. In "Survival-of-the-flattest", organisms that occupy flat (but not terribly high) fitness peaks can outcompete populations that live on high (and very pointy) peaks, but only when the mutation rate is high enough (see schematic drawing in the figure below).


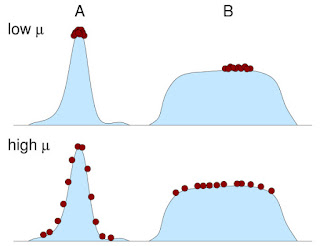Survival of the flattest. At low mutation rate (top panel), the population living on peak A outcompetes the one living on peak B. At high mutation rate (lower panel), the steepness of peak A implies that many of the mutants on that peak have very low fitness, and the population as a whole will therefore grow poorly. The population on peak B, on the other hand, has mostly neutral mutants, and will outcompete the population at A. (Figure courtesy of Claus Wilke). 

Because of this "lower fitness outcompeting higher fitness" business, the effect violates the semi-edict of "ever-increasing information/fitness". It is a semi-law because, truthfully, nobody ever really declared it a law. It is a "most-of-the-time" law, much like the second law of thermodynamics, come to think of it.


The effect we'll discuss presently concerns population size rather than mutation rate, and just like the "survival-of-the-flattest" effect it violates the semi-edict; the almost-law. We shall call this new effect "survival-of-the-steepest". It goes without saying that this lame attempt at analogizing with the survival-of-the-flattest moniker couldn't be more obvious. But since that original moniker was due to Rich Lenski, and he did not object to this particular use, we'll just run with it and see if it sticks. (It may not.)

Come to think of it, Lenski had suggested an even better pun for this effect: "Drift Dodger". You'll appreciate that one more after digesting the stuff below. "Survival of the drift dodger". It could work, no?


So let's first talk a little bit about small populations. You remember, of course, that evolution is something that happens in populations. The reason why it cannot happen to a single isolated individual is the essence of one of the three components of the Darwinian Triad: selection. If there is only one organism, then you cannot have differential survival. There are no differences, because there is only one. You cannot win if there is no competition.


If you have two individuals, you could in principle have evolution because there can be differences between the two. Yet, I'm sure I can convince you that it will be extremely difficult for evolution to proceed in this contrived case. The reason for this is that organisms can die. Yes, you read that right: if organisms could not die, then two would be enough to sustain an evolutionary process in principle. But death is inevitable in a finite world with replication, so that settles that. Actually, let me be more precise: death, by itself, does not prevent evolution in small populations. It is instead random death that thwarts evolution, because if death only affected the lower fitness type, then evolution could still work with only two individuals. However, if death strikes randomly, then half the time the fitter one of the pair would be removed, and the one left over then replicates to restore the pair. Because the less-fit individual got to reproduce, the overall population fitness has declined.  This is the essence of genetic drift. Now imagine one of the pair is again struck by a mutation. We know that there are far more mutations that reduce fitness than there are those that increase fitness (it is easier to break things by chance than to improve them by random changes). After such a mutation, there is a new lower fitness organisms, and if death strikes randomly, there is again a fifty/fifty chance that the lower fitness organism remains.


You can now understand that, unless beneficial mutations are at least as common as deleterious mutations, this process of a gradual loss of fitness will doom the population. And in the case I just described, this is precisely Muller's ratchet, an inexorable decline in fitness that will doom the small population to extinction. In this extreme example this happened to a population of two, but the process happens anytime the population is extremely small (say, 10 or smaller in most cases).

It turns out that here is a way to resist this decline, but for a population to resist it, it must "live" on a particular type of fitness peak: one with steep slopes. The steeper, the better.

Imagine you have a population that has been dropped into a fitness landscape that has only two peaks: a lower one with steep slopes, and a higher one with gentle slopes (as in the picture below).

A small population will not be able to climb the peek with gentle slopes, because genetic drift will prevent small advances to fix. However, such a population will be able to climb peaks with steep slopes (such as the one on the left) because selection is effective for large advances.

A large population will find itself on the blue peak with gentle slopes, because the population that climbed the red peak will be forced into extinction due to the higher fitness of the blue peak. However, if the population size is small, the tables are turned. The small population will not be able to ascend the blue peak, as drift will consistently (and without doubt annoyingly) "throw it back down": mutations with small effect cannot go to fixation when the population size is small. But that intrepid small population can climb the red peak, because it requires big steps to get up there. It might take a while to discover these steps, but once they are found, the population will safely occupy and maintain itself on the the steep peak. This means that this population is robust to drift on such a peak. Were we to transplant the same population to the blue peak it could not maintain itself there, and drift back down that gentle slope. On the red, steep, peak, however, the population is robust to drift. It can dodge the drift. There you have it.

So now we have seen that there are two important exceptions to the "survival of the fittest" rule, the law that stipulates that those genotypes that replicate the fastest should always be the ultimate winners of the competition. This rule holds only at very small mutation rates, and for very large population sizes.

Is there is a more general rule that predicts the winner even at finite mutation rates and small population sizes? A universal law, in a way, that holds without restrictions in mutation rate and population size? I believe that there is such a law indeed, but you'll have to wait for another blog post to find out what it is! That law (I am teasing) is inspired by thermodynamics, which tells us that that small energy (just as high fitness) is not always the winner. That law will set fitness free once and for all.

The research described in this post is based on the paper linked to below. It is openly accessible to everyone.

T. LaBar and C. Adami, "Evolution of drift robustness in small population", Nature Communications 8 (2017) 1012.

An evolutionary theory of music

"The beauty of music is in the ear of the beholder", we are always told. Or perhaps we are not always told this, but I imagine that we should be told that. Because while I like a lot of music that other people like, I don't always agree with what other people say is--not just music--but insist is "good" music. I'm unabashedly a "romanticist": I love the piano concertos of Rachmaninov, and most of what Chopin wrote. I'm a Beethoven guy, but I have learned to like Bach, and there is some stuff that Mozart wrote that should be in the Hall of Fame of Music, compared to all music ever written. 

But when it comes to Stravinsky, Schönberg, Alban Berg, or Karlheinz Stockhausen, I'm at a loss. I don't understand it. It doesn't sound like music to me. 

Is it them, or is it me? Is there something about the music that the aforementioned composers wrote that is too complex for my brain? What is the complexity of music, anyway? Is it obvious that some music is just more complicated than some other music, and that it takes more sophisticated brains than mine to appreciate the postmodern kind of music?

I have to say that there is some evidence in favor of the position that, yes, my brain is just not sophisticated enough to appreciate Stockhausen. That I'm just not bright enough for Berg. Too rudimentary for Rautevaara. You get the drift.

The evidence is multifaceted. As a young lad, I just simply assumed that I was right in loathing all this "modern music" nonsense (even though I had rehearsed Britten's War Requiem as a 11-year old, a memory that I would only recover much later). I liked Beethoven, Rachmaninov, and Chopin. Then I saw a piece on TV that would change my perception of music forever. I saw a "Harvard Lecture" by Leonard Bernstein, a director and all-around musical genius that I admired (I was perhaps 18). It is one of the now famous "The Unanswered Question" Lectures of Bernstein (but I did not know that when I saw it.) Bernstein lectured about Schoenberg (as he spelled his name after he moved to the US). I can still remember my astonishment, as he took apart Schoenberg's  "Verklärte Nacht" and lectured me about its structure, and pointed out the references to earlier classical music (sometimes inverted). I realized then and there that I had been extremely naive about music. 

Arnold Schoenberg, by Egon Schiele
Source: Wikimedia

That does not mean that I immediately came to like Schoenberg's music. I was still wondering whether anybody really liked it, as opposed to appreciate it on an intellectual level.

Then came the time when I was called to sing Stravinsky. 

We are performing a formidable jump here, from my formative years to a period where I was a Full Professor at the Keck Graduate Institute, a university specializing in Applied Life Sciences in Claremont, California.  They had a choir there, and as I had sung in a choir as an 11-year old (culminating in the aforementioned Britten episode that never resulted in a performance) I figured I'd get Mozart's Requiem off of my bucket list. I admit I'm a bit obsessed with this piece of music. I perhaps know way too much about it at this point. Anyway, the Claremont College Choir was going to perform it, so I signed up. (Well, you don't just sign up: you have to audition, and pass.)

During the audition, I was asked to sing some fairly atonal stuff. I had no inkling whatsoever that the choir director was testing me on Stravinsky's Symphony of Psalms. But after I was admitted to the choir, I learned that this was the piece we were going to perform alongside the Requiem.  

I bought the CD, and listened to it on my daily commute from Pasadena to Claremont. At first, it sounded like cats were being drowned. I later asked people who were at the performance, and got similar reactions. I thought I could never never sing that. So I broke out Garageband or Logic Pro and wrote the bass track (that was the voice I was to sing) onto the music, so that I could rehearse it. 

With practice, the unthinkable happened. I started to understand the music. I started to like it. I started to be moved by it. I slowly realized that this was great music, and that I was completely incapable to have realized this upon first hearing it.

This is, by the way, a dynamic that is not completely limited to music. Similar things can happen to you in the appreciation of mathematics. There is some mathematics that is utterly obvious. It is obviously beautiful, and everybody usually appreciates that beauty. Simple number theory, for example. The zeta function. But then I found that there was mathematics that I could not easily grasp. There is no beauty in mathematics that you do not understand. It may look like gibberish to you, as if the author just juxtaposed symbols with the intent to obfuscate. I still believe that there is mathematics out there that is just gibberish, but the beauty lies in those pieces that you learn to appreciate after "listening" to them for as long as it takes until you start to understand them.

So, our brains (certainly mine) are not exactly reliable judges of beauty. What is beauty anyway?

If you start to think about this question, you've got to take into consideration evolutionary forces. What we call "beauty", or "beautiful", is something that appeals to us, and there are plenty of reasons why we should be manipulated by something appealing. Countless prey have been lured into demise thusly. So what appeals to us?

The answer to this is (at least this is my answer): "We like that which we can predict".

Many many pages have been written about how our brain processes information, but for me, the most convincing narrative is due to Jeff Hawkins, entrepreneur and neuroscientist, who I have written about several times in this blog (perhaps most notably in its very first installment--and second--, immortalizing our very first meeting).

What Jeff taught me (first in his breathtaking book "On Intelligence", and later in person) is that our brains are primarily prediction machines. Our brains predict the future, and we love it when we are right. We hate it when we are not. Let me give you the example I learned from Jeff's book, and which I have repeated countless times.

Walking, you may think, is easy. Those who have tried to make robots walk will tell you it is not. How do we do it, then? It turns out that bipedal walking relies on a complex sensory-motor interplay, and this is not the post to dwell on its details. But we know from experiment the following: if you lose the sense of touch in your feet, your gait will be severely affected. Basically, you'll stumble, rather than walk. Why is this?

It turns out that while you are happily conversing with the person next to you while walking, your brain subconsciously makes hundreds of predictions about what your sensory systems will experience next. And when it comes to walking, it makes predictions about the exact timing of the impact of the ground with your feet. Your brain does this for every step (but of course you do not realize that, because of the "unconscious" part). And every time that your foot experiences the ground (via your feet's sensors) at precisely the predicted time, your brain (subconsciously) says "Aaaah."

Your brain likes it when its predictions are fulfilled. It is happy when anticipation is actualized. Because when all is as predicted, then all is well. And when all is well, our brain does not need to waste precious energy on attending to details, when important things have to be addressed.

But what if there is a rut in the road, or a lump in the lane? In those cases, the anticipated impact of the foot with the road will be delayed (rut) or early (lump), and our brain immediately springs to attention. The prediction was not realized, and our brain (correctly) interprets this as a harbinger of trouble. If my prediction was incorrect (so argues your brain) in this instance, it might be incorrect in the next, and this means that we need to pay close attention to the situation at hand. And so, reacting to this alert, you now inspect the path you are trodding with much more care, to learn about the imperfections you hitherto ignored, and to learn to anticipate those too.

This little example, I'm sure you see immediately, is emblematic of how our brain processes all sensory information, including visual, and for the purpose of this blog post, auditory, information.

According to this view, our brain is happiest if it can anticipate the next sounds. And, when it comes to music, this predisposition of our brain begins to explain a lot about how we process music. After all, the structure of repetitions in almost all forms (I should say, Western) forms of music is uncanny. We like repetition, and we (dare I say it) think it is beautiful. Not too much repetition, mind you. But it is now clear that we like repetition because it makes music predictable. This is also why, we now realize much more clearly, we begin to like music after we have heard it a couple of times. And yes, some music is so simple, so derivative, so instantly recognized that we also like it instantly, upon first hearing. But perhaps we can now also understand that this is not the kind of music that requires any artistry.

How much repetition is best? Is there an optimum that has just enough repetition that we can barely predict it (creating the happiness of correct prediction) and evades the boredom of the obvious repetition that does not tax us, but annoys instead?  If this is true, shouldn't an evolutionary process be able to optimize it?

Yes, you can evolve music. You can do this yourself right now, by moseying over to evolectronica, where you can click on audio loops and rate them. The average rating will determine the  number of offspring any of the tunes in the population will obtain (suitably mutated, of course). Good tunes will prosper in this world. I have nothing to do with this site, but I did write about a paper that studied how such loops evolve. That paper was published in the Proceedings of the US National Academy of Sciences (link here), and turns out to be an interesting application of evolutionary genetics. My commentary, highlighting the importance of epistasis between genetic traits, was published in the same journal, at this link.

In the paper linked above, the authors use two traits to quantify the fitness of music: the "tonal clarity", and the 'rhythmic complexity". They find that while during early evolution the overall musical appeal of the tunes increases as each of these traits increase, the appeal then flattened out. During the time, neither clarity or appeal increased, seemingly holding each other back (see the qualitative rendition of the process in the figure below).

Evolutionary trajectory of tunes under selection (from [1]). Evolution does not reach maximum fitness because traits interact, and likely because other traits like predictability are not considered. Figure by B. Østman.

In the light of what we just discussed, maybe the failure to maximize fitness (in terms of musical appeal) is not surprising. Brains do prefer variation, but not too much. Average brains (such as mine) certainly do not prefer super-complicated rhythms. Yes, we like complexity, but complexity that remains predictable. We enjoy challenges, as long as they remain leisurely. Stravinsky is a challenge both in tonal clarity and rhythmic complexity. It can be mastered, but it requires formidable repetition.

So what is good music? That, it appears, will always remain in the brain of the beholder, simply because different brains have different capacities to predict. Some of us will love the simplest of tunes because they stick with us immediately. Some others love the challenge of trying to understand a piece that even after one hundred listens cannot be whistled.

I've whistled Stravinsky's Symphony of Psalms, so anything is possible!


[1] R. M. MacCallum, M. Mauch, A. Burt, and A. M. Leroi, Evolution of music by public choice. Proc. Natl. Acad. Sci. USA 109 (2012) 12081-12086.
[2] C. Adami, Adaptive walks on the fitness landscape of music. Proc. Natl. Acad. Sci. USA 109 (2012) 11898–11899.

What can the physics of spin crystals tell us about how we cooperate?

In the natural world, cooperation is everywhere. You can see it among people, of course, but not everybody cooperates all the time. Some people, as I'm sure you've heard or experienced, don't really care for cooperation. Indeed, if cooperation were something that everybody does all the time, we wouldn't even talk about it: we'd take it for granted.

But we cannot take it for granted, and the main reason for this has to do with evolution. Grant me, for a moment, that cooperation is an inherited behavioral trait. This is not a novelty mind you: plenty of behavioral traits are inherited. You may not be completely aware that you yourself have such traits, but you sure do recognize them in animals, in particular courtship displays and all the complex rituals associated with them. So if a behavioral trait is inherited, it is very likely selected for because it enhances the organisms's fitness. But the moment you think about how cooperation as a trait may have evolved, you hit a snag. A problem, a dilemma. 

If cooperation is a decision that promotes increased fitness if two (or more) individuals engage in it, it must be just as possible to not engage in it. (Remember, cooperation is only worth talking about if it is voluntary.) The problem arises when in a group of cooperators an individual decides not to cooperate. It becomes a problem because that individual still gets the benefit of all the other individuals cooperating with them, but without actually paying the cost of cooperation.  Obtaining a benefit without paying the cost means you get mo' money, and thus higher fitness. This is a problem because if this non-cooperation decision is an inherited trait just as cooperation is, well then the defector's kids (a defector is a non-cooperator) will do it too, and also leave more kids. And the longer this goes on, all the cooperators will have been wiped out and replaced by, well, defectors. In the parlance of evolutionary game theory, cooperation is an unstable trait that is vulnerable to infiltration by defectors. In the language of mathematics, defection--not cooperation--is the stable equilibrium fixed point (a Nash equilibrium). In the language of you and me: "What on Earth is going on here?" 

Here's what's going on. Evolution does not look ahead. Evolution does not worry that "Oh, all your non-cooperating nonsense will bite you in the tush one of these days", because evolution rewards success now, not tomorrow. By that reasoning, there should not be any cooperating going on among people, animals, or microbes for that matter. Yet, of course, cooperation is rampant among people (most), animals (most), and microbes (many). How come?

The answer to this question is not simple, because nature is not simple. There are many different reasons why the naive expectation that evolution cannot give rise to cooperation is not what we observe today, and I can't here go into analyzing all of them here. Maybe one day I'll do a multi-part series (you know I'm not above that) and go into the many different ways evolution has "found a way". In the present setting, I'm going to go all "physics" with you instead, and show you that we can actually try to understand cooperation using the physics of magnetic materials. I kid you not.

Cooperation occurs between pairs of players, or groups of players. What I'm going to show you is how you can view both of these cases in terms of interactions between tiny magnets, which are called "spins" in physics. They are the microscopic (tiny) things that macroscopic (big) magnets are made out of. In theories of ferromagnetism, the magnetism is created by the alignment of electron spins in the domains of the magnet, as in the picture below.

Fig. 1: Micrograph of the surface of a ferromagnetic material, showing the crystal "grains", which are areas of aligned spins (Source: Wikimedia).

If the temperature were exactly zero, then in principle all these domains could align to point in the same direction, so that the magnetization of the crystal would be maximal. But when the temperature is not zero (degrees Kelvin, that is), then the magnetization is less than maximal. As the temperature is increased, the magnetization of the crystal decreases, until it abruptly vanishes at the co-called "critical temperature". It would look something like the plot below.

Fig. 2: Magnetization M of a ferromagnetic crystal as a function of temperature T (arbitrary units). 

"That's all fine and dandy", I hear you mumble, "but what does this have to do with cooperation?" And before I have a chance to respond, you add: "And why would temperature have anything to do with how we cooperate? Do you become selfish when you get hot?"

All good questions, so let me answer them one at a time. First, let us look at a simpler situation, the "one-dimensional spin chain" (compared to the two-dimensional "spin-lattice"). In physics, when we try to solve a problem, we first try to solve the simplest and easiest version of the problem, and then we check whether the solution we came up with actually applies to the more complex and messier real world. A one-dimensional chain may look like this one:

Fig. 3: A one-dimensional spin chain with periodic boundary condition

This chain has no beginning or end, so that we don't need to deal with, well, beginnings and ends. (We can do the same thing with a two-dimensional crystal: it then topologically becomes a torus.)

So what does this have to do with cooperation? Simply identify a spin-up with a cooperator, and a spin-down with a defector, and you get a one-dimensional group of cooperators and defectors:

                                                C-C-C-D-D-D-D-C-C-C-D-D-D-C-D-C

Now, asking what the average fraction of C's vs. D's on this string is, becomes the same thing as asking what is the magnetization of the spin chain! All we need is to write down how the players in the chain interact. In physics, spins interact with their nearest neighbors, and there are three different values for "interaction energies", depending on how the spins are oriented. For example, you could write

$$E(\uparrow,\uparrow)=a,       E(\uparrow,\downarrow)=E(\downarrow,\uparrow)=b,  E(\downarrow,\downarrow)=c$$.

which you could also write into matrix form like so:
$$E=\begin{pmatrix} a & b\\ b& c\\ \end{pmatrix}$$

And funny enough, this is precisely how payoff matrices in evolutionary game theory are written! And because payoffs in game theory are translated into fitness, we can now see that the role of energy in physics is played by fitness in evolution. Except, as you may have noted immediately, that in physics the interactions lower the energy, while in evolution, Darwinian dynamics maximizes fitness. How can the two be reconciled?

It turns out that this is the easy part. If we replace all fitnesses by "energy=max_fitness minus fitness", then fitness maximization is turned into energy minimization. This can be achieved simply by taking a payoff matrix such as the one above, identifying the largest value in the matrix, and replacing all entries by "largest value minus entry". And in physics, a constant added (or subtracted) to all energies does not matter (remember when they told you in physics class that all energies are defined only in relation to some scale? That's what they meant by that.)

"But what about the temperature part? There is no temperature in game theory, is there?"

You're right, there isn't. But temperature in thermodynamics is really just a measure of how energy fluctuates (it's a bit more complicated, but let's leave it at that). And of course fitness, in evolutionary theory, is also not a constant. It can fluctuate (within any particular lineage) for a number of reasons. For example, in small populations the force that maximizes fitness (the equivalent of the energy-minimization principle) isn't very effective, and as a result the selected fitness will fluctuate (generally, decrease, via the process of genetic drift). Mutations also will lead to fitness fluctuations, so generally we can say that the rate at which fitness fluctuates due to different strengths of selection can be seen as equivalent to temperature in thermal physics.

One way to model the strength of selection in game theory is to replace the Darwinian "strategy inheritance" process (a successful strategy giving rise to successful "children-strategies") with a "strategy adoption" model, where a strategy can adopt the strategy of a competing individual with a certain probability. Temperature in such a model would simply quantify how likely it is that an individual will adopt an inferior strategy. And it turns out that "strategy adoption" and "strategy inheritance" give rise to very similar dynamics, so we can use strategy adoption to model evolution. And low and behold, the way the boundaries between groups of aligned spins change in magnetic crystals is precisely by the "spin adoption" model, also known as Glauber dynamics. This will become important later on.

OK, I realize this is all getting a bit dry. Let's just take a time-out, and look at cat pictures. After all, there is nothing that can't be improved by looking at cat pictures.  Here's one of my cat eyeing our goldfish:

Fig. 4: An interaction between a non-cooperator with an unwitting subject

Needless to say, the subsequent interaction between the cat and the fish did not bode well for the future of this particular fish's lineage, but it should be said that because the fish was alone in its bowl, its fitness was zero regardless of the unfortunate future encounter.

After this interlude, before we forge ahead, let me summarize what we have learned.

1. Cooperation is difficult to understand as being a product of evolution because cooperation's benefits are delayed, and evolution rewards immediate gains (which favor defectors).

2. We can study cooperation by exploiting an interesting (and not entirely overlooked) analogy between the energy-minimization principle of physics, and the fitness-maximizing principle of evolution.

3. Cooperation in groups with spatial structure can be studied in one dimension. Evolutionary game theory between players can be viewed as the interaction of spins in a one-dimensional chain.

4. The spin chain "evolves" when spins "adopt" an alternative state (as if mutated) if the new state lowers the energy/increases the fitness, on average.

All right, let's go a-calculating! But let's start small. (This is how you begin in theoretical physics, always). Can we solve the lowly Prisoner's Dilemma?

What's the Prisoner's Dilemma, you ask? Why, it's only the most famous game in the literature of evolutionary game theory! It has a satisfyingly conspiratorial name, with an open-ended unfolding. Who are these prisoners? What's their dilemma? I wrote about this game before here, but to be self-contained I'll describe it again.

Let us imagine that a crime has been committed by a pair of hoodlums. It is a crime somewhere between petty and serious, and if caught in flagrante, the penalty is steep (but not devastating). Say, five years in the slammer. But let us imagine that the two conspires were caught fleeing the scene independently, leaving the law-enforcement professionals puzzled. "Which of the two is the perp?", they wonder. They cannot convene a grand jury because each of the alleged bandits could say that it was the other who committed the deed, creating reasonable doubt. So each of the suspects is questioned separately, and the interrogator offers each the same deal: "If you tell us it was the other guy, I'll slap you with a charge of being in the wrong place at the wrong time, and you get off with time served. But if you stay mum, we'll put the screws on you." The honorable thing is, of course, not to rat out your compadre, because they will each get a lesser sentence if the authorities cannot pin the deed on an individual. But they also must fear being had: having a noble sentiment can land you behind bars for five years with your former friend dancing in the streets. Staying silent is a "cooperating" move, ratting out is "defection", because of the temptation to defect. The rational solution in this game is indeed to defect and rat out, even though for this move each player gets a sentence that is larger than if they both cooperated. But it is the "correct" move. And herein lies the dilemma.

A typical way to describe the costs and benefits in this game is in terms of a payoff matrix:

Here, b is the benefit you get for cooperation, and c is the cost. If both players cooperate, the "row player" receives b-c, as does the "column" player. If the row player cooperates but the column player defects, the row-player pays the cost but does not reap the reward, for a net -c. If the tables are reversed, the row player gets b, but does not pay the cost at they just defected. If both defect, they each get zero. So you see that the matrix only lists the reward for the row player (but the payoff for the column player is evident from inspection).

We can now use this matrix to calculate the mean "magnetization" of a one-dimensional chain of Cs and Ds, by pretending that \({\rm C}=\uparrow\) and \({\rm D}=\downarrow\) (the opposite identification would work just as well). In thermal physics, we calculate this magnetization as a function of temperature, but I'm not going to show you in detail how to do this. You can look it up in the paper that I'm going to link to at the end. Yes I know, you are so very surprised that there is a paper attached to the blog post. Or a blog post attached to the paper. Whatever.

Let me show you what this fraction of cooperators (or magnetization of the spin crystal) looks like:

Fig. 5: "Magnetization" of a 1D chain, or fraction of cooperators, as a function of the net payoff \(r=b-c\), for three different temperatures. 

You notice immediately that the magnetization is always negative, which here means that there are always more defectors than there are cooperators. The dilemma is immediately obvious: as you increase \(r\), meaning that there is increasingly more benefit than cost), the fraction of defectors actually increases. When the net payoff increases for cooperation, you would expect that there would be more cooperation, not less. But the temptation to defect increases also, and so defection becomes more and more rational.

Of course, none of these findings are new. But it is the first time that the dilemma of cooperation was mapped to the thermodynamics of spin crystals. Can this analogy be expanded, so that the techniques of physics can actually give new results?

Let's try a game that's a tad more sophisticated: the Public Goods game. This game is very similar to the Prisoner's Dilemma, but it is played by three or more players. (When played by two players, it is the same as the Prisoner's Dilemma). The idea of this game is also simple. Each player in the group (say, for simplicity, three) can either pay into a "pot" (the Public Good), or not. Paying means cooperating, and not paying (obviously) is defection. After this, the total Public Good is multiplied by a parameter that is larger than 1 (we will call it r here also), which you can think of as a synergy effect stemming from the investment, and the result is then equally divided to all players in the group, regardless of whether they paid in or not.

Cooperation can be very lucrative: if all players in the group pay in one and the synergy factor r=2, then each gets back two (the pot has grown to six from being multiplied by two, and those six are evenly divided to all three players). This means one hundred percent ROI (return on investment). That's fantastic! Trouble is, there's a dilemma. Suppose Joe Cheapskate does not pay in. Now the pot is 2, multiplied by 2 is 4. In this case each player receives 1 and 1/3 back, which is still an ROI of 33 percent for the cooperators, not bad. But check out Joe: he paid in nothing and got 1.33 back. His ROI is infinite. If you translate earnings into offspring, who do you think will win the battle of fecundity? The cooperators will die out, and this is precisely what you observe when you run the experiment. As in the Prisoner's Dilemma, defection is the rational choice. I can show this to you by simulating the game in one dimension again. Now, a player interacts with its two nearest neighbors to the left and right:

The payoff matrix is different from that of the Prisoner's Dilemma, of course. In the simulation, we use "Glauber dynamics" to update a strategy. (Remember when I warned that this was going to be important?) The strength of selection is inversely proportional to what we would call temperature, and this is quite intuitive: if the temperature is high, then changes are so fast and random that selection is very ineffective because temperature is larger than most fitness differences. If the temperature is small, then tiny differences in fitness are clearly "visible" to evolution, and will be exploited.

The simulations show that (as opposed to the Prisoner's Dilemma) cooperation can be achieved in this game, as long as the synergy factor r is larger than the group size:

Fig. 6: Fraction of cooperators in a computational simulation of the Public Goods game in one dimension. Here T is the inverse of the selection strength. As $T\to0$, the change from defection to cooperation becomes more and more abrupt. There are error bars, but they are too small to be seen. 

This graph shows that there is an abrupt change from defection to cooperation as the synergy factor is increased, and this change becomes more and more abrupt the smaller the "temperature", that is, the larger the strength of selection. This behavior is exactly what you would expect in a phase transition at a critical r=3, so it looks that this game also should be describable by thermodynamics.

Quick aside here. If you just said to yourself "Wait a minute, there are no phase transitions in one dimension" because you know van Hove's theorem, you should immediately stop reading this blog and skip right to the paper (link below) because you are in the wrong place: you do not need this blog. If, on the other hand, you read "van Hove" and thought "Who?", then please keep on reading. It's OK. Almost nobody knows this theorem.

Alright, I said we were going to do the physics now. I won't show you how exactly, of course. There may not be enough cat pictures on the Internet to get you to follow this. <Checks>. Actually, I take that back. YouTube alone has enough. But it would still take too long, so let's just skip right to the result.

I derive the mean fraction of cooperators as the mean magnetization of the spin chain, which I write as \(\langle J_z\rangle_\beta\). This looks odd to you because none of these symbols have been defined here. The J refers to a the spin operator in physics, and the z refers to the z-component of that operator. The spins you have seen here all point either up or down, which just means \(J_z\) is minus one or plus one here. The \(\beta\) is a common abbreviation in physics for the inverse temperature, that is, \(\beta=1/T\). And the angled brackets just mean "average".  So the symbol \(\langle J_z\rangle_\beta\) is just reminding you that I'm not calculating average fraction of cooperators. I am calculating the magnetization of a spin chain at finite temperature, which is the average number of spins-up minus spins-down. And I did all this by converting the payoff matrix into a suitable Hamiltonian, which is really just an energy function.

Mathematically, the result turns out to be surprisingly simple:
$$\langle J_z\rangle=\tanh[\frac\beta2(r/3-1)] \ \ \  (1)$$  
Let's plot the formula, to check how this compares to simulating game theory on a computer:

Fig. 7: The above formula, plotted against r for the different inverse temperatures $\beta$.

OK, let's put them side-by-side, the simulation, and the theory:

You'll notice that they are not exactly the same, but they are very close. Keep in mind that the theory assumes (essentially) an infinite population. The simulation has a finite population (1,024 players), and I show the average of 100 independent replicate simulations, that ran for 2 million updates, meaning that each of the sites of the chain was updated about 2,000 times each.

Even though they are so similar, how they were obtained could hardly be more different. The set of curves on the left was obtained by updating "actual" strings many many times, and recording the fraction of Cs and Ds on them after doing this 2 million times. (This, as any computational simulation you see in this post, was done by my collaborator on this project, Arend Hintze).  To obtain the curve on the right, I just used a pencil, paper, and an eraser. It shows off the power of theory, because once you have a closed-form solution such as Eq. (1) above, not only does this solution tell you some important things, but you can now imagine using the formalism to do all the other things that are usually done in spin physics, and that we never would have thought of doing if all we did was simulate the process.

And that's exactly what Arend Hintze and I did: we looked for more analogies with magnetic materials, and whether they can teach you about the emergence of cooperation. But before I show you one of them, I will mercifully throw in some more cat pictures. This is my other cat, the younger one. She is in a box, and no, Schrödinger had nothing to do with it. Cats just like to sit in boxes. They really do.

Our cat Alex has appropriated the German Adventskalender house

All right, enough with the cat entertainment. Let's get back to the story. Arend and I had some evidence from a previous paper [1] that this barrier to cooperation (namely, that the synergy has to be at last as large as the group size) can be lowered if defectors can be punished (by other players) for defecting. That punishment, it turns out, is mostly meted out by other cooperators, because being a defector and a punisher at the same time turns out to be an exceedingly bad strategy. I'm honestly not making a political commentary here. Honest. OK, almost honest.

And thinking about punishment as an "incentive to align", we wondered (seeing the analogy between the battle between cooperators and defectors, and the thermodynamics of low-dimensional spin systems) whether punishment could be viewed like a magnetic field that attempts to align spins in a preferred direction.

And that turned out to be true. I will spare you again the  technical part of the story (which is indeed significantly more technical), but I'll show you the side-by-side of the simulation and the theory. In those plots, I show you only one temperature \(T=0.2\), that is \(\beta=5\). But I show three different fines, meaning punishments with different strength of effect, here labelled as \(\epsilon\). The higher \(\epsilon\), the higher the "pain" of punishment on the defector (measured in terms of reduced payoff).

When we did the simulations, we also included a parameter that is the cost of punishing others. Indeed, doing so subtracts from a cooperator' net payoff: you should not be able to punish others without suffering a little bit yourself. (Again, I'm not being political here.) But we saw little effect of cost on the results, while the effect of punishment really mattered. When I derived the formula for the magnetization as a function of the cost of punishment \(\gamma\) and the effect of punishment \(\epsilon\), I found:
$$\langle J_z\rangle=\frac{1-\cosh^2(\beta\frac\epsilon4)e^{-\beta(\frac r3+\frac\epsilon2-1)}}{1+\cosh^2(\beta\frac\epsilon4)e^{-\beta(\frac r3+\frac\epsilon2-1)}} \ \ \        (2)$$
Keep in mind, I don't expect you to nod knowingly when you see that formula. What I want you to notice is that there is no \(\gamma\) there. But I can assure you, it was there during the calculation, but during the very last steps it miraculously cancelled out of the final equation, leaving a much simpler expression than the one that I had carried through from the beginning.

And that, dear reader, who has endured for so long, being propped up and carried along by cat pictures no less, is the main message I want to convey. Mathematics is a set of tools that can help you keep track of things. Maybe a smarter version of me could have realized all along that the cost of punishment \(\gamma\) will not play a role, and math would have been unnecessary. But I needed the math to tell me that (the simulations had hinted at that, but it was not conclusive).

Oh, I now realize that I never showed you the comparison between simulation and theory in the presence of punishment (aka, the magnetic field). Here it is (simulation on the left, theory on the right:

So what is our take-home message here? There are many, actually. A simple one tells you that to evolve cooperation in populations, you need some enabling mechanisms to overcome the dilemma. Yes, a synergy larger than the group size will get you cooperation, but this is achieved by eliminating the dilemma, because when the synergy is that high, not contributing actually hurts your bottom line. Here the enabling mechanism is punishment, but we need to keep in mind that punishment is only possible if you can distinguish cooperators from defectors (lest you punish indiscriminately). This ability is tantamount to the communication of one bit of information, which is the enabling factor I previously wrote about when discussing the Prisoner's Dilemma with communication. Oh and by the way, the work I just described has been published in Ref. [2]. Follow the link, or find the free version on arXiv.

A less simple message is that while computational simulations are a fantastic tool to go beyond mathematics--to go where mathematics alone cannot go [3]--new ideas can open up new directions that will open up new paths that we thought could only be pursued with the help of computers. Mathematics (and physics) thus still has some surprises to deliver to us, and Arend and I are hot on the trail of others. Stay tuned!


References

[1] A. Hintze and C. Adami, Punishment in Public Goods games leads to meta-stable phase transitions and hysteresis, Physical Biology 12 (2005) 046005.
[2] C. Adami and A. Hintze, Thermodynamics of evolutionary games. Phys. Rev. E 97 (2018) 062136
[3] C. Adami, J. Schossau, and A. Hintze, Evolutionary game theory using agent-based methods, Phys. Life Reviews. 19 (2016) 38-42.

Are quanta particles or waves?

The title of this post is an age-old question isn't it? Particle or wave? Wave or particle? Many have rightly argued that the so-called "wave-particle duality" is at the very heart of quantum weirdness, and hence, of all of quantum mechanics. Einstein said it. Bohr said it. Feynman said it. Two out of those three are physics heroes of mine, so that's a majority right there.

Feynman, when talking about what we now call the wave-particle duality, was referring to the famous "double-slit experiment". He wrote (in his famous Feynman Lectures, Chapter 37 of Volume 1, to be precise):

Richard Feynman (1918-1988)
Source: Wikimedia

"We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery. We cannot make the mystery go away by “explaining” how it works. We will just tell you how it works. In telling you how it works we will have told you about the basic peculiarities of all quantum mechanics."

So what is Feynman talking about here? Instead of launching on a lengthy exposition of the double-slit experiment, as luck would have it I've already done that, in a blog post about the quantum eraser. That post, incidentally, was No. 6 in the "Quantum measurement" series that starts here. You don't necessarily have to have read all those posts to follow this one, but believe me, it would help a lot. At the minimum, start at No. 6 if you're not already familiar with the double-slit experiment. But you'll get a succinct introduction to the double-slit experiment below anyway.

Alright, back to quantum mechanics. Actually, step back a little bit more, to classical mechanics. In classical physics, there is no duality between waves and particles. Waves are waves, and they would never behave like particles. For example, you can't kick a wave, really, no matter what the surfer types tell you. Particles on the other hand, do not interfere with each other as waves do. You can kick particles (kinda), and you can count them. You can't count waves. 

What Bohr, Einstein, and Feynman are trying to tell you is that in quantum mechanics (meaning the real world, because as I have told you before, classical mechanics is an illusion, it does not exist) the same stuff can be either particle OR wave. Not both, mind you. Here's what Einstein said about this, and to tell you the truth, this statement sounds like he's been hanging out with Bohr far too much:

A. Einstein (1879-1955)
Source: Wikimedia

"It seems as though we must use sometimes the one theory and sometimes the other, while at times we may use either. We are faced with a new kind of difficulty. We have two contradictory pictures of reality; separately neither of them fully explains the phenomena of light, but together they do".

I've used a picture of Einstein in 1904 here, because you've seen far too many pics of him sticking out his tongue and hair disheveled. He wasn't like that most of the time when he made his most important contributions.

Lest you think that the troubles these 20th-century physicists had with quantum mechanics are the stuff of history, think again. In 2012, a mere 5 years ago, experimenters from Germany (in the lab of the very eminent Wolfgang Schleich) claimed that they had collected evidence that a quantum system can be both particle and wave at the same time. Such an observation-if true-would run afoul of Bohr's "duality principle", which declared that a quantum system can only be one or the other, depending on the type of experiment used to examine the system. One or the other, but never both. 

Rest assured though, analyzing results of the Schleich experiment in a different way reveals that all is well with complementarity after all, as was pointed out by a team at the University of Ottawa, led by the equally eminent Robert Boyd. (You can read an excellent summary of that controversy in Tom Siegfried's piece here.) What all this fighting about duality should teach you is that this is not at all a solved problem. As recently as a few days ago, Steven Weinberg (who, full disclosure, has also been in my pantheon of physicists ever after I read his "First Three Minutes" at a very tender age) wrote about the particle-wave duality in the New York Review of Books. I hope that he reads this post, because it may alleviate some of his troubles.  

In his piece entitled "The Trouble with Quantum Mechanics", Weinberg admits to being as puzzled as his predecessors Einstein, Bohr, and Feynman, about the true nature of quantum physics. How can we understand, he muses, that quantum dynamics is governed by a deterministic equation (the Schrödinger equation), yet when we try to measure something, then all we can muster is probabilities? "So we still have to ask", Weinberg writes, "how do probabilities get into quantum mechanics?"

How indeed. You know of course, from reading my diatribes, that this is a question I am interested in myself. I have obliquely hinted that I think I know where the probabilities are coming from (if you can find the relevant post) and that one day I'll write a detailed account of that idea (it's 3/4 written already, actually). But today is not that day. Having convinced you that the particle-wave duality is still a very hot topic in quantum physics, let me take on that particular subject first. 

What I want to do in this blog post is to make you think differently about the complementarity principle. What I'm going to tell you is that you should stop thinking in terms of "particle or wave". It is a false dichotomy. It is a false dilemma because quantum systems are neither particle nor wave. Those two are classical concepts, after all. Strictly speaking, quantum systems are quantum fields. But this is not the time to delve into quantum field theory, so instead I will try to marshal the tools of quantum information theory to tell you what is really complementary in quantum measurement, what it is that you can have "only one of", and what it is that is being "traded-off". You don't exchange a bit of particle for a bit of wave, this much I can tell you right here. 

To do this, I have to introduce you to some very counter-intuitive quantum stuff. Now, you might argue: "All quantum stuff is counter-intuitive", and I'd have to agree with you if all your intuition is classical. What I am going to tell you is stuff that even baffles seasoned quantum physicists. I'm going to tell you about quantum experiments where the "nature" of the quantum experiment that you perform can be changed after you've already completed the experiment!

Let me remind you right here, that the--also very eminent--Niels Bohr tried to teach us that whether a quantum system appears as a particle or as a wave depends on the type of experiment you subject it to. Here I'm telling you that this is a bunch of hogwash, because I'll show you that when you do an experiment, you can change whether it is a "particle"- or a "wave"-experiment long after the data have been collected!

I know you're not shocked at my dissing Bohr as I have a habit of doing so. But I'm in good company, by the way, if you read what Feynman wrote about Bohr in his "Surely You're Joking" series. 

"Alright I bite", one of you readers exclaimed just now, "how do you retroactively change the type of experiment you make?" 

Glad you asked. Because now I can talk about John Archibald Wheeler. Wheeler was not a conventional physicist: Even though his early career as a nuclear physicist led to several important contributions to the Manhattan project, he was also interested in many other areas of physics. Indeed, he was a central figure in the "revival" of general relativity theory. (That theory had gone a bit out of fashion when people realized that many predictions of the theory were difficult to measure.) Wheeler co-authored what many (including myself) think is the best book on the topic: "Gravitation" (with Charles Misner and Kip Thorne). That book is often just referred to as "MTW".

John Archibald Wheeler (1911-2008).
Source: University of Texas

I never got to meet Wheeler, perhaps because I entered the field of quantum gravity too late. While Wheeler has been influential in the field of quantum information, it really was his gravity work that had the most lasting impact. He invented the terms "black hole" and "wormhole", after all. His most influential contribution to quantum information science is, undoubtedly, the "delayed choice" gedankenexperiment. Let me explain that to you. 

Wheeler's thought experiment examines the question of whether a photon, say, takes on wave or particle nature before it interacts with the experiment, sensing (in a way) what kind of experiment is going to be performed on it. In the simplest version of the delayed choice experiment, the nature of the experiment would be changed "after the photon had made up its mind" whether it was going to play the role of particle, or whether it would make an appearance as a wave. Needless to say, this is of course not how quantum mechanics works, and Wheeler was fully aware of it. His interpretation was that a photon is neither wave nor particle, and that it takes on one of the two "coats" only when it is being observed. I'm going to tell you that I agree with the first part (the photon is neither wave nor particle), but I disagree with the second part: it does not in fact take on either particle or wave nature after it is observed. It never ever takes on such a role.

If you think about it, the idea that a system only "comes into being by being observed" is preposterous (however, such a thought was quite in line with some other of Wheeler's philosophies). Measurements are interactions with other systems just as much as any other interactions are: there is nothing special about measurement. This is, in essence, what I'm going to try to convince you of. 

Even though the reasoning behind the delayed-choice experiment is preposterous, it has generated an enormous amount of work. Let's first look at how we may set up such an experiment. Below is an illustration of a double-slit experiment from Feynman's famous lecture, where he replaced photons by electrons shot out of an electron gun (such devices are perfectly reasonable and feasible). Note that Caltech, where Feynman spent the majority of his career, has made these lectures freely available. The particular chapter can be accessed here. 

Fig. 1: An interference experiment with electrons. (Source: Feynman Lectures on Physics)

Later on, we're going to be using photons instead of electrons for the quantum system, because experiments are much easier with photon beams as opposed to electron beams.  In that case, we are going to assume that any light is going to be so faint that it can't be thought of as the classical light waves that give rise to Young's interference fringes. Then, at any point in time, there will be at most one photon between the double-slit and the detector, so you have to think about single photons either taking one or the other, or both paths, through the double-slit experiment. 

Quantum mechanics predicts that a single electron takes both paths to create the interference pattern in the figure above at (c). Thus, it must somehow interfere with itself, which is difficult to imagine if you think of the electron as a particle. (Which of course it is not). Can we force it to behave as a particle? Suppose you put a particle detector between the wall and the backstop: one behind slit 1, and one behind slit 2. If you get a "hit" on either detector, then you know on which path the electron traveled. (You can do this experiment without actually removing the electron, so that you can still get patterns on the screen.) When you obtain this "which-path" information, the interference pattern disappears: you've forced the electron to behave as a particle. We discussed this earlier in Part 6 of the "On quantum measurement" series.

Wheeler's idea was this: Suppose the distance between the wall and the backstop is very, very large. If you do not put the contraption that will measure which path the electron took (the "which-path detector") into the experiment, the electron would have no choice but to go along both paths, ready to interfere with itself and create the interference pattern on the screen. But suppose you bring in the "which-path" apparatus after the electron has passed the slit, but before it is going to hit the screen. Is the electron wave function that is on the "other path" going to "change its mind", or go backwards? What would happen? The thought experiment very nicely illustrates how preposterous the idea is that the experiment itself determines "what the quantum system is", as changing the experiment mid-flight cannot possibly change the nature of the electron.

The experiment I'm going to describe to you (the delayed-choice quantum eraser experiment) has in fact been carried out several times now, and drives Wheeler's idea to the extreme. The choice of experiment (insert the "which-path" detector or not), can be made after the electron has hit the screen! If you are a reader for whom this is immediately obvious, then congratulations (and consider a career in quantum physics, if this is not already your career). It is indeed completely obvious if you understand quantum mechanics, but let me walk you through it anyway. 

First, if it was the experiment that determines the nature of the quantum system (particle or wave), how can you change the experiment after it already has occurred? That this is possible is also due to the peculiarities of quantum physics, and it is also the hardest to explain. I'll do it with photons rather than electrons, as this is the experiment that was carried out, and it is also the description I used in the paper that I'm really writing about. You knew this was coming, didn't you?

We can do double-slit experiments with photons just as with electrons: we just have to turn down the intensity of light such that individual photons can be registered on a phosphorescent screen. When you see the screen light up at a particular spot (or, in more modern times, a pixel on a CCD detector lights up), you interpret it that a photon has hit there. Often, the double-slit is replaced by a Mach-Zehnder interferometer, but you shouldn't worry about such technicalities: you can in fact use either. 

To pull off this feat of changing the experiment after the fact, you have to create an entangled pair of photons first. You already know what an entangled pair (a "Bell-state") is, because I wrote about it several times: for example in the context of black holes here, and in the context of quantum teleportation and superdense coding here. This pair of photons is also sometimes called an Einstein-Podolsky-Rosen (EPR) pair, because that trio first described a similar entangled state in a very famous paper in 1935. 

Let's create such a pair by entangling the "polarization" degree of freedom of the photon. This is the part that is a bit more complicated: to understand it, you have to understand polarization. 

Every photon can come in two different polarization states, but what these states are depends on how you decide to measure them. This will be crucial, because this is in fact how you change the measurement after the fact. The thing to know about an entangled pair is that it is in a superposition of those two states. Suppose we use as basis for the photon polarization the "horizontal/vertical" basis. That means that if a photon is polarized horizontally, and you put a filter in front of it that only allows vertical polarization to go through, then out comes nothing. Polarization is, if you will, a photon's way of wiggling. Below is a picture that shows the photon wiggling in the "vertical" and in the horizontal way. But they can also wiggle in the "circular-left" and "circular-right" way. In fact, it can wiggle in an infinite number of "opposing ways", and these are related to each other by a unitary transformation. 

Fig. 2: One way of depicting photon polarization. 

The way a photon is polarized can be changed by an optical element (a "wave plate"), and this ability will be key in the experiment. Suppose we begin with a pair of photons A and B in a Bell-state, written in terms of the horizontal \(|h\rangle\) and vertical \(|v\rangle\) polarization eigenstates:

\(|\Psi\rangle_{AB}=\frac1{\sqrt2}(|h\rangle_A|v\rangle_B+|v\rangle_A|h\rangle_B)\)          (1)    

You notice that neither of the photons has a defined state, but if I measure one of them (say A) and find that my detector says it is in an \(|h\rangle\) state, then I can be sure that measuring B will give you "v", no matter whether you do the measurement now, or a year later with a detector placed a light-year away. This is precisely what Einstein could not stomach, calling this mysterious bond "spooky action at a distance", but a careful analysis reveals that there is no "action" at all: signals cannot be sent using this bond. 

But here's the thing: I can measure photon B either in the h,v coordinate system, or in another one. This will become crucial, so keep this in mind. But for the moment let's forget that a "copy" of photon A (the entangled partner) is flying out there, possibly to a measurement device a light-year away. Actually, there is nothing a light year away from us, so let's say we are far in the future and the detector is on Proxima Centauri, about 4 and a quarter light-years away. It'll just be a longer experiment. 

Photon A now goes through a double-slit, just as the electrons in Figure 1. Now we'll do the "are you a particle or a wave" measurement. We do this by putting a so-called "quarter-wave plats" into the path of one of the photons. When you do this, you entangle the polarization of the photon with the spatial degree of freedom (namely "left slit" or "right slit"). Once you've done this, you only have to measure the polarization of photon A to know whether it went through the left or right slit. In a way, you've tagged the photon's path by the polarization. After doing this, you will lose the interference pattern. You can either have an interference pattern (and we say that the photon wavefunction is "coherent"), or you can have "which-path" information, which makes the wavefunction incoherent. Or so people thought for a long time. It turns out that you can also have a little bit of both, but you can't have both full which-path information, and full coherence: there is a tradeoff. And that tradeoff depends on the angle by which you rotate the polarization basis. In the description above, we used a "quarter-wave" plate, which gives you full information, and zero coherence. Choose something other than 45 degrees (that's the quarter-wave), and you can get a little bit of both. 

It turns out that there is a simple relationship that quantifies this tradeoff in terms of the angle you choose to do the tagging with. Let's call this angle \(\phi\). We can then define the "distinguishability" D and the "visibility" V, where \(D^2\) measures how well you can distinguish the photon paths (a measure of which-path information), while \(V^2\) quantifies the visibility of the interference fringes (a measure of the coherence of the wavefunction). A celebrated inequality (due to Greenberger and Yasin [1]) states that

\(D^2+V^2\leq1\)     (2)

Now, according to what I just wrote, choosing the angle of the wave plate when performing the which-path entangling operation chooses the experiment for you: Set it at 0 degree and you do not entangle at all, so that no which-path information is obtained (then \(D^2=0\) and \(V^2=1\)). Set it at \(\phi=\pi/4\), and you get perfect which-path information, and no visibility. How can you choose the experiment after the fact, when you have to choose the angle when setting up the experiment? How?

So the following is what makes quantum mechanics so beautiful. You can actually do this because when I described the experiment to you, I did not (it turns out) use an entangled EPR pair as the input, I used a photon in a defined polarization state, such as \(|h\rangle\). I did not tell you about this because it would have confused you. I needed you to understand how to extract which-path information first, and how doing it gradually will gradually destroy coherence. 

Now take a deep breath, and read very slowly.

If the input to the two-slits (and therefore to the "which-path" detector that entangles polarization and path) is the EPR state Eq. (1), you actually do not get any which-path information using the quarter-wave plate. This is because when the photon "comes in", it is not in a defined polarization state at all. If it was not in a defined state, you extract nothing. So for that setup, \(V^2=1\) even though \(\phi=\pi/4\). 

Now one more deep breath after you digested this bit. Maybe take two, just to be safe. 

Whether the state that impinges on to the two slits is indeed Eq. (1) is up to the person at Proxima Centauri, four-and-a-quarter years after that data was recorded on the CCD screen on Earth.  This is because what is \(|h\rangle\) and what is \(|v\rangle\) is determined by how you measure it. A quantum system does not have a state until you say how you measure it. It will be in the h,v basis if that is the basis of your measurement device. It will be in the R,L  (right-circular, left-circular) basis, if that is instead what you will choose to examine it with. Or it could be anything in between.

I wrote about this at length in the blog post about the collapse of the wavefunction, within the "On quantum measurement" series. (Rightfully, the present post really should be "On quantum measurement. Part 8, but I decided to make it stand-alone). Please go back to that if the two breaths did not help. There is also an intriguing parallel to how Shannon entropy is not defined until you determine how you will be measuring it, as I wrote about in "What is Information-Part 1".  The deeper reason for this is that all of physics is about the relative state of measurement devices. Mark my words. 

The reason our person at Proxima Centauri handling photon B actually prepares the state is because photon A is not "projected" at any point of the experiment. This could be done, of course, but that is a different experiment. So now we can see how the delayed-choice experiment works: If Proxima Centauri person (PCP, for short) measures at an angle \(\theta=0\) with respect to the preparation Eq. (2), then the photon is in a defined state (no matter whether the outcome is h or v) and only then do you actually extract which-path information. In that case, visibility \(V^2=0\). If PCP measures at \(\theta=\pi/4\) on the other hand, the entanglement operation (the "tagging") does not work: it is as if the measurement by PCP "erased" the tagging, and \(V^2=1\) instead. So indeed, a measurement far in the future (well, here more than four years in the future) will determine what kind of an experiment is done on the photon. The event far in the future will determine whether the photon appeared as a particle, or a wave. Weird, right? 

What is that you ask? How can an event far in the future affect the data that are stored on a device far in the past? 

I didn't say it did, did I? Of course it does not. The truth is much more magical. Without going into all the details here (but which you can read about in any paper about the Bell-state quantum eraser, or indeed my own paper referenced below), the result of the measurement by PCP in the future contains crucial information about how to decode the data in the past, information that is akin to the key in a cryptography procedure. 

Yes, cryptographic. That is indeed what I wrote. You will only be able to decipher \(D^2\) and \(V^2\) when the measurement in the future (which is really a state preparation in the past) is available to you. That is the true magic of quantum mechanics. Without it, you won't be able to see any fringes in the data. But with it, you may be able to reconstruct them to full visibility, if that is how the photon was measured at Proxima Centauri. 

How do I know any of this is true? Because we (my student Jennifer Glick and I) analyzed the entire experiment in terms of quantum information theory, and ultimately were able to write down the equations that describe discrimination and visibility (coherence) entirely in terms of entropies and information, in [2] (Jennifer did all the calculations and wrote the first draft of the manuscript). Clearly, "which-path information" should have an obvious information-theoretic rendering, but it turns out that this is actually a little bit tricky because it really is a "conditional information". But it turns out that "coherence" (or "visibility") can also be measured information-theoretically. And lo and behold, the two are related. In our description, they are related by a common information-theoretic identity: the chain rule for entropies. According to that identity, information I and coherence C (as a function of the PCP angle \(\theta\)) are related so that

 

\(I(\theta)+C(\theta)=1\)        (3) .

In a simple qubit model, the information and coherence take on extremely simple forms, namely \(I(\theta)=H[\sin^2(\theta+\pi/4)]\) with \(C(\theta)=1-H[\sin^2(\theta+\pi/4)]\), where \(H[p]\) is the standard Shannon entropy function \(H[p]=-p\log(p)-(1-p)\log(1-p)\). And take a look at how our information-theoretic quantities compare to the quantum optical measures of discrimination and visibility in Fig. 3 below. It almost looks like that discrimination and visibility (coherence) should have been defined information-theoretically from the outset, doesn't it?

Fig.3: Top: Which-path information (solid line) and coherence (dashed line) in terms of quantum information theory. Bottom: Discrimination (solid) and visibility (dashed)  in quantum optics. Q refers to the quantum state at the beam-splitter, and \(D_A\)  and \(D_B\) refer to polarization detectors. From [2].  

So what does all this teach us about quantum mechanics, in the end (besides, of course, that quantum mechanics is awesome)? We have learned at least two things. Quantum systems are not either particle or wave. They are in fact neither because both concepts are classical in nature. This, to some extent, I stipulate we knew already. Wheeler knew it.  (Bohr, I contend, not so much). But what I've shown you is that quantum systems don't "change their colors" after measurement either, as Wheeler had advocated. They remain "neither", even when we think we pinned them down, because what I've shown you is that you can have them take on this coat or that, or any in between, years after the ink has dried (I mean, after the data were recorded). They (the photons, electrons, etc.) are not one or the other. They appear to you the way you choose you want to see them, when you interrogate a quantum state with classical devices. 

Those devices cannot reveal to you the reality of the quantum state, because the devices are classical. Don't hate them because of their limitations. Instead, use them wisely, because what I just showed you is that, if used in a clever manner, they enable you to learn something about the true nature of quantum physics after all. As, for example, the experiment in [3] does.

References

[1] D.M. Greenberger and A. Yasin, "Simultaneous wave and particle knowledge in a neutron interferometer. Physics Letters A 128 (1988) 391-394.
[2] J.R. Glick and C. Adami, "Quantum information theory of the Bell-state quantum eraser". Phys. Rev. A 95 (2017) 012105. Full text also on arXiv. 
Note: Jennifer Glick is first author on this paper because she performed all calculations in it and wrote the first draft. 
[3] Y.H. Kim, R. Yu, S.P. Kulik, Y.H. Shih, and M.O. Scully, “Delayed “choice” quantum eraser,” Phys Rev Lett 84 (2000) 1-5.