So Part 7 wasn't the final installment in this series after all. I know this because this is Part 8 of the quantum measurement saga. And for this one, I'm going to change the style a bit. I will begin with a fictional dialogue between two quantum physicists, called "Lenny" and "Chris". After the dialogue, I will delve more deeply into what it is that Lenny and Chris are talking about.
This is a dialogue between Lenny and Chris, two fictional physicists. Both know quantum physics. They both can calculate things. But Lenny has an advantage: he can also do experiments. He has made a discovery, and wants to show it to Chris.
Lenny: "Hey Chris, I just wrote down this equation describing a series of three consecutive measurements on the same quantum system. My equation says that when you make these three measurements 'a', 'b', and 'c', a particular sum must always be smaller or equal to 1."
Chris: "Wow Lenny, this looks great. It looks like a solid prediction. You should try and check that. You know, because of your ability to measure things. In quantum physics."
Lenny: "You know what, I'm going to do just that.
Time passes. Music is playing in the background. It is mildly annoying. A while later:
Lenny: Hey, that's actually a difficult experiment. Doing two measurements in a row is easy, but doing three is hard. Do you think I can instead do three different measurements where I just do a pair of measurements in each?"
Chris: "What do you mean?"
Lenny: "Here I'll sketch it for you on the board"
Time passes. Music is playing in the background. It is mildly annoying. A while later:
Lenny: Hey, that's actually a difficult experiment. Doing two measurements in a row is easy, but doing three is hard. Do you think I can instead do three different measurements where I just do a pair of measurements in each?"
Chris: "What do you mean?"
Lenny: "Here I'll sketch it for you on the board"
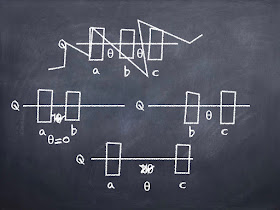
Lenny: "Here's the quantum state \(Q\), and here's the three measurements, see? Let's call them a, b, and c. And we should do each measurement at an angle \(\theta\) with respect to the previous measurement"
Chris: "Yup. Go on."
Lenny: "Well, I wanted to just do the pairs, 'ab', 'bc', and 'ac', like so:
Lenny: "See, I first do the first pair just like above. Then I do the "bc" measurement (but I don't really have to because it is really just the same as the "ab" measurement), and then I do the one at the bottom of the chalkboard, where I leave out the middle one."
Chris: "Ah but Lenny, leaving out the middle measurement changes everything. It's, like, the first lesson in quantum mechanics. Measurements change the system that is being measured. That's why we have the uncertainty relation".
Lenny: "But what if the middle measurement doesn't matter?"
Chris: "What?"
Lenny: "Hear me out. What if I did the experiment and assume that I get the same result as if I had done the measurement? As if the middle measurement didn't matter."
Chris: "You mean, like in classical physics?"
Lenny: "Yes, just as in classical physics".
Chris: "But we already know that measurements like this cannot be described by classical physics".
Lenny: "I'll just say I'm testing "classical thinking".
Chris: "Sure, you could do that. But nobody thinks that classical thinking will get the same result, so you'll never be able to publish such a result."
More time passes. A lot of time. Finally Lenny is back. He is out of breath. The blackboard, miraculously, has not been erased.
Lenny: "Chris, you're not going to believe it. I did those three pairs of measurements and I get a result that's different from what quantum mechanics predicts for doing all three measurements!"
Chris: "Actually, Lenny, I totally believe it. It is what quantum mechanics predicts after all."
Lenny: "But it's much better than that! The results are such that the equation that quantum mechanics says can never exceed one, actually does! I broke the inequality!"
Chris: "That is not possible. Show me what you did."
Lenny: "I did the measurements just like on the board."
Chris: "You did? What angles did you use?"
Lenny: "I used \(\theta\) for the angle between the first two and also between the last two, and \(2\theta\) between the first and the third, assuming the middle one does not matter."
Chris: "Yeah, you can't do that."
Lenny: "What?"
Chris: "The three experiments are supposed to mimic the experiment at the top of the blackboard, right?
Lenny: "Yes. And as long as I prepare each of the three experiments exactly in the same manner, I can use the statistics of the three pairwise measurements to stand in for the triple one."
Chris: "That is true. But you didn't prepare your three measurements in the same way. You used very different parameters in each. That is not allowed."
Lenny: "What do you mean? Angle \(\theta\) between the first two and the last two, and angle \(2\theta\) between the first and third. It's the same."
Chris: "It is not. Let me explain."
Lenny: "See, I first do the first pair just like above. Then I do the "bc" measurement (but I don't really have to because it is really just the same as the "ab" measurement), and then I do the one at the bottom of the chalkboard, where I leave out the middle one."
Chris: "Ah but Lenny, leaving out the middle measurement changes everything. It's, like, the first lesson in quantum mechanics. Measurements change the system that is being measured. That's why we have the uncertainty relation".
Lenny: "But what if the middle measurement doesn't matter?"
Chris: "What?"
Lenny: "Hear me out. What if I did the experiment and assume that I get the same result as if I had done the measurement? As if the middle measurement didn't matter."
Chris: "You mean, like in classical physics?"
Lenny: "Yes, just as in classical physics".
Chris: "But we already know that measurements like this cannot be described by classical physics".
Lenny: "I'll just say I'm testing "classical thinking".
Chris: "Sure, you could do that. But nobody thinks that classical thinking will get the same result, so you'll never be able to publish such a result."
Lenny: "Oh but I bet I can. I just won't call it 'classical thinking'. I'll call it macrorealism. I'll say I'm testing macrorealist theories.''
Chris: "Now you're just trolling me. But go ahead knock yourself out."
Chris: "Now you're just trolling me. But go ahead knock yourself out."
Lenny: "Chris, you're not going to believe it. I did those three pairs of measurements and I get a result that's different from what quantum mechanics predicts for doing all three measurements!"
Chris: "Actually, Lenny, I totally believe it. It is what quantum mechanics predicts after all."
Lenny: "But it's much better than that! The results are such that the equation that quantum mechanics says can never exceed one, actually does! I broke the inequality!"
Chris: "That is not possible. Show me what you did."
Lenny: "I did the measurements just like on the board."
Chris: "You did? What angles did you use?"
Lenny: "I used \(\theta\) for the angle between the first two and also between the last two, and \(2\theta\) between the first and the third, assuming the middle one does not matter."
Chris: "Yeah, you can't do that."
Lenny: "What?"
Chris: "The three experiments are supposed to mimic the experiment at the top of the blackboard, right?
Lenny: "Yes. And as long as I prepare each of the three experiments exactly in the same manner, I can use the statistics of the three pairwise measurements to stand in for the triple one."
Chris: "That is true. But you didn't prepare your three measurements in the same way. You used very different parameters in each. That is not allowed."
Lenny: "What do you mean? Angle \(\theta\) between the first two and the last two, and angle \(2\theta\) between the first and third. It's the same."
Chris: "It is not. Let me explain."
So what are Lenny and Chris talking about here? They are discussing making consecutive measurements on the same quantum system, something that we encountered already in Part 7, which is linked. While I describe the theory of consecutive measurements in that part, with a focus on whether or not wavefunctions collapse during measurements, that part of the theory is completely irrelevant for the following. Collapse and no-collapse pictures make the same predictions for what follows.
Let's first set up the three measurements. For convenience, we'll take a quantum two-state system (a qubit) and all our detectors are binary detectors (they click or they don't). There are of course many ways in which we can realize such a series of measurement, and one of the simplest is via a Mach-Zehnder optical setup. You've seen versions of it several times in this series.
 |
| Fig. 1: Measuring the quantum system \(|\Psi_1\rangle\) using the classical detectors \(A_1\), \(A_2\), and \(A_3\). |
Here, the dark grey boxes with an angle written on top are polarizing beam splitters set at an angle with respect to the polarization of the initial state. You can think of these polarizing beam splitters to change the basis of the quantum state, so that for example, \(A_2\) measures the quantum state at a relative angle \(\theta_1\) compared to \(A_1\), and \(A_3\) measures at angle \(\theta_2\) with respect to \(A_2\). I'm sure you realized by now that these three measurements are just the 'a', 'b', and 'c' of the dialogue.
If you don't want to think in terms of interferometers, you can also just look at the quantum circuit in Fig. 2.
Alright, so what is this equation that Lenny and Chris are discussing. It concerns the correlation between pairs of detectors. For example, I might want to know what the correlation is between detectors 1 and 2. I call this function \(K_{12}\). It's fairly simple to derive it, but I won't do it here. It's described in detail in the paper that I'll be linking to. Don't groan, you knew this was coming.
For example, suppose \(\theta_1=0\). This means that \(A_1\) and \(A_2\) measure in the same basis, and quantum mechanics then tells us that both detectors must agree. So \(K_{12}(0)=1\). On the contrary, if \(\theta_1=\pi/2\), then you are measuring at orthogonal angles and the correlation must vanish. Indeed quantum mechanics predicts
We can also calculate \(K_{23}\) in this manner. You get the same result, only with the angle \(\theta_2\), that is, \(K_{23}=\cos(\theta_2)\).
What about \(K_{13}\)? Well, this result will depend on whether or not we make the 'b' measurement in between. If we do it, then the result is
\(K_{13}=\cos(\theta_1)\cos(\theta_2)\;.\) (2)
If instead we don't do it, then the third measurement will occur at the angle \(\theta_1+\theta_2\) with respect to the first, and we then should find \(K_{13}=\cos(\theta_1+\theta_2)\).
There is, by the way, no controversy about the result of these calculations. They are easy to do. Doing or not doing a measurement matters. Everybody knows that. I assume you are nodding vigorously in assent. You did, didn't you?
Let me now write down the equation that Chris and Lenny have been discussing.
It can be shown, using the formalism I introduced in Part 7 (or any other standard quantum measurement formalism, for that matter) that the following inequality holds:
\(K_{12}+K_{23}-K_{13}\leq1\;.\) (3)
This is only one of the so-called "Leggett-Garg inequalities", introduced by Sir Anthony Leggett and Anupam Garg [1] , but for the sake of being brief it is the only one I'm going to consider here.
Like I wrote above, whether or not you are making two or three measurements matters. Let's find out how. First, let us check what we get for the inequality if all three measurements are performed. Using the results above, and assuming that \(\theta_1=\theta_2\equiv\theta\), that is, I'm choosing the same change in basis between the first and the second, as the second and third measurement), we get
\(2\cos(\theta)-\cos^2(\theta))\leq1\;.\) (4)
It's immediately clear that this inequality cannot be violated, because the left hand side of Eq. (4) is \(1-(1-\cos(\theta))^2\), which is less than one for all \(\theta\). There is no way that Equation (3) can ever be violated, even if you use two different angles \(\theta_1\) or \(\theta_2\).
But Lenny said that he did violate inequality (3), and all he had to do was not make the middle measurement. If that would be true, quantum mechanics would be broken because equation (3) should hold whether or not I'm making the middle measurement.
OK, what does it mean to *not* make a measurement? There are actually two ways in which you could do that (of course they turn out to be the same). One way to do this is to actually *do* the measurement, but you must make it at the same angle that you made the first measurement. You choose any other value, and the second measurement *is* made. But remember, in the 'ac' measurement you are not doing the second one, and since in order to simulate the triple measurement you must do all three pairwise experiments with the same parameter values, then if you do not measure at position 'b' in the third measurement (for the 'ac' correlation), you must also not make that measurement in the first of the three also (for the 'ab' correlation). And the second (for the 'bc' correlation) just the same.
Otherwise, those three pairwise measurements do not describe the triple-measurement situation, and the inequality does not describe this set of measurements. So instead, what you should do is this:
You're not doing the 'b' measurement, so you have to choose \(\theta=0\) for the 'ab' measurement. You are doing the 'bc' measurement at angle \(\theta\). That's fine. But the angle between the first (non-measurement) and the third is then \(\theta\), not \(2\theta\). Because 0 plus \(\theta\) is \(\theta\).
If you use these angles and plug them in to equation (3), you immediately realize that the inequality is not violated: it is exactly equal to 1. If you want to use \(2\theta\) for the third ('ac') measurement instead, then you also have to use that angle in the 'bc' measurement, since the first measurement (at 'b') had to be done at zero angle. You can't say that you don't do a measurement (for the 'ac') experiment, yet do it in the 'ab' measurement, and believe that it describes the same experiment (the 'abc' measurement). It's like saying I use \(\theta=45\) degrees in the 'ab' measurement, but I use \(\theta=30\) in the 'ac' measurement. You can't just change angles if you want the statistics of the pairwise measurements to reflect the full triple measurement. If you do, then the three pairwise measurements are not standing in for the triple measurement.
I told you earlier that there was another way of *not* doing a measurement. This is making a measurement so weakly that it becomes non-existent. What's a weak measurement you ask? It's actually a simple concept, and I'll briefly explain it here.
At the risk of repeating myself, here's what happens in a measurement. You want to move the measurement device's "needle" in such a manner that it reflects the thing that you want to measure. If what you are measuring has only two states, then (for example) you want to keep the measurement device as is when the system is in one of the states, and you want to move the measurement device into a different state if the system is in the other. If you want to make sure which is which, you need to make sure that the two states of the measurement device are easily distinguishable. In quantum physics, the best you can do (for distinguishability) is to make the two states orthogonal. Indeed that is precisely what you do in projective measurements.
But it is possible to make measurements where you don't move the measurement device's "needle" by 90 degrees (into the orthogonal direction). What if you just move it a little?
If you move the device's needle just a little, then it becomes harder to make sure what the device's state is after measurement. Say you move the needle by an angle \(\phi\). Because your device at this point is just another qubit, then in order to amplify your measurement (make it available to a classical reader) you need to measure it again. But this time using an orthogonal device. This means there is a change that the ancillary qubit will be misread. (This is not possible if the measurement was done at an angle 90 degrees, that is, a strong measurement).
A weak measurement, therefore, is a fuzzy measurement. You might think that this is a terrible way of doing a measurement, but there are plenty of uses for this. For one, you can make this measurement more precise by repeating it many times. If you do, you can detect even very small angles \(\phi\). What you gained is that your weak measurement only weakly disturbed the quantum system. OK, so let's do some weak measurements. To prepare you for that, I'm going to magnanimously repeat strong measurements, as if you did not already read Parts 1-7. I know you did, but who can remember things from so long ago?
\(K_{12}+K_{23}-K_{13}=1\;\)
the same result we obtained when we didn't do the second measurement by choosing the first \(\theta=0\). Whichever way we choose not to do the middle measurement (because we want to simplify our work by doing only pairs of measurements), the Leggett-Garg inequalities cannot be violated. Ever.
What does all this mean for us? Well, people have wondered over and over again why it is so easy to violate inequalities that should be observed by quantum mechanics. Some (including Leggett) have suggested that when it comes to macroscopic phenomena, quantum mechanics can't be the right theory. Of course, you might say, we use classical mechanics there. But you need to remember that classical mechanics is not a correct theory. We need to be able to describe classical objects with quantum mechanics, or at least something that both describes microscopic and macroscopic objects accurately at the same time. Others have suggested that quantum mechanics is indeed the right theory, but that we just haven't (for a variety of reasons) been able to observe the deviations that the violation of LG inequalities implies. One of the reasons suggested by that camp is that perhaps we can never really perform perfectly strong measurements, and that this ``fuzziness" of measurements might obscure the violations [2]. Instead, we now realize that there are no paradoxes at all. Quantum mechanics correctly describes both microscopic and macroscopic physics. And we see no "weird" stuff in quantum measurement of macroscopic devices not because strong measurements can't be achieved, but because those violations simply do not exist. They are based on the faulty thinking that plagued Lenny. I do realize that there are literally hundreds of papers that follow Lenny's thinking in making pairwise experiments. All of them claim the Leggett-Garg inequalities are violated. All of them are wrong.
The preprint describing this work is [3] below. I have applied this thinking to the so-called "entropic" Leggett-Garg inequalities, which are related to the original inequalities but distinct. In [4] I show that these can't be violated either.
[1] A. J. Leggett and A. Garg, “Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks?” Phys. Rev. Lett. 54, 857–860 (1985).
[2] J. Kofler and C. Brukner, “Conditions for quantum violation of macroscopic realism,” Phys. Rev. Lett. 101, 090403 (2008).
[3] C. Adami, “Leggett-Garg inequalities cannot be violated in quantum measurements,” arXiv:1908.02866 (2019)
[4] C. Adami, “Neither weak nor strong entropic Leggett-Garg inequalities can be violated,” arXiv:1908.03124 (2019).
For example, suppose \(\theta_1=0\). This means that \(A_1\) and \(A_2\) measure in the same basis, and quantum mechanics then tells us that both detectors must agree. So \(K_{12}(0)=1\). On the contrary, if \(\theta_1=\pi/2\), then you are measuring at orthogonal angles and the correlation must vanish. Indeed quantum mechanics predicts
\(K_{12}=\cos(\theta_1)\;.\) (1)
We can also calculate \(K_{23}\) in this manner. You get the same result, only with the angle \(\theta_2\), that is, \(K_{23}=\cos(\theta_2)\).
What about \(K_{13}\)? Well, this result will depend on whether or not we make the 'b' measurement in between. If we do it, then the result is
\(K_{13}=\cos(\theta_1)\cos(\theta_2)\;.\) (2)
If instead we don't do it, then the third measurement will occur at the angle \(\theta_1+\theta_2\) with respect to the first, and we then should find \(K_{13}=\cos(\theta_1+\theta_2)\).
There is, by the way, no controversy about the result of these calculations. They are easy to do. Doing or not doing a measurement matters. Everybody knows that. I assume you are nodding vigorously in assent. You did, didn't you?
Let me now write down the equation that Chris and Lenny have been discussing.
It can be shown, using the formalism I introduced in Part 7 (or any other standard quantum measurement formalism, for that matter) that the following inequality holds:
\(K_{12}+K_{23}-K_{13}\leq1\;.\) (3)
This is only one of the so-called "Leggett-Garg inequalities", introduced by Sir Anthony Leggett and Anupam Garg [1] , but for the sake of being brief it is the only one I'm going to consider here.
Like I wrote above, whether or not you are making two or three measurements matters. Let's find out how. First, let us check what we get for the inequality if all three measurements are performed. Using the results above, and assuming that \(\theta_1=\theta_2\equiv\theta\), that is, I'm choosing the same change in basis between the first and the second, as the second and third measurement), we get
\(2\cos(\theta)-\cos^2(\theta))\leq1\;.\) (4)
It's immediately clear that this inequality cannot be violated, because the left hand side of Eq. (4) is \(1-(1-\cos(\theta))^2\), which is less than one for all \(\theta\). There is no way that Equation (3) can ever be violated, even if you use two different angles \(\theta_1\) or \(\theta_2\).
But Lenny said that he did violate inequality (3), and all he had to do was not make the middle measurement. If that would be true, quantum mechanics would be broken because equation (3) should hold whether or not I'm making the middle measurement.
OK, what does it mean to *not* make a measurement? There are actually two ways in which you could do that (of course they turn out to be the same). One way to do this is to actually *do* the measurement, but you must make it at the same angle that you made the first measurement. You choose any other value, and the second measurement *is* made. But remember, in the 'ac' measurement you are not doing the second one, and since in order to simulate the triple measurement you must do all three pairwise experiments with the same parameter values, then if you do not measure at position 'b' in the third measurement (for the 'ac' correlation), you must also not make that measurement in the first of the three also (for the 'ab' correlation). And the second (for the 'bc' correlation) just the same.
Otherwise, those three pairwise measurements do not describe the triple-measurement situation, and the inequality does not describe this set of measurements. So instead, what you should do is this:
You're not doing the 'b' measurement, so you have to choose \(\theta=0\) for the 'ab' measurement. You are doing the 'bc' measurement at angle \(\theta\). That's fine. But the angle between the first (non-measurement) and the third is then \(\theta\), not \(2\theta\). Because 0 plus \(\theta\) is \(\theta\).
If you use these angles and plug them in to equation (3), you immediately realize that the inequality is not violated: it is exactly equal to 1. If you want to use \(2\theta\) for the third ('ac') measurement instead, then you also have to use that angle in the 'bc' measurement, since the first measurement (at 'b') had to be done at zero angle. You can't say that you don't do a measurement (for the 'ac') experiment, yet do it in the 'ab' measurement, and believe that it describes the same experiment (the 'abc' measurement). It's like saying I use \(\theta=45\) degrees in the 'ab' measurement, but I use \(\theta=30\) in the 'ac' measurement. You can't just change angles if you want the statistics of the pairwise measurements to reflect the full triple measurement. If you do, then the three pairwise measurements are not standing in for the triple measurement.
I told you earlier that there was another way of *not* doing a measurement. This is making a measurement so weakly that it becomes non-existent. What's a weak measurement you ask? It's actually a simple concept, and I'll briefly explain it here.
At the risk of repeating myself, here's what happens in a measurement. You want to move the measurement device's "needle" in such a manner that it reflects the thing that you want to measure. If what you are measuring has only two states, then (for example) you want to keep the measurement device as is when the system is in one of the states, and you want to move the measurement device into a different state if the system is in the other. If you want to make sure which is which, you need to make sure that the two states of the measurement device are easily distinguishable. In quantum physics, the best you can do (for distinguishability) is to make the two states orthogonal. Indeed that is precisely what you do in projective measurements.
But it is possible to make measurements where you don't move the measurement device's "needle" by 90 degrees (into the orthogonal direction). What if you just move it a little?
If you move the device's needle just a little, then it becomes harder to make sure what the device's state is after measurement. Say you move the needle by an angle \(\phi\). Because your device at this point is just another qubit, then in order to amplify your measurement (make it available to a classical reader) you need to measure it again. But this time using an orthogonal device. This means there is a change that the ancillary qubit will be misread. (This is not possible if the measurement was done at an angle 90 degrees, that is, a strong measurement).
A weak measurement, therefore, is a fuzzy measurement. You might think that this is a terrible way of doing a measurement, but there are plenty of uses for this. For one, you can make this measurement more precise by repeating it many times. If you do, you can detect even very small angles \(\phi\). What you gained is that your weak measurement only weakly disturbed the quantum system. OK, so let's do some weak measurements. To prepare you for that, I'm going to magnanimously repeat strong measurements, as if you did not already read Parts 1-7. I know you did, but who can remember things from so long ago?
Here we imagine that our quantum system is prepared. This means that we took an arbitrary quantum state, and measured it with a particular device. No matter what the outcome of that "preparing" step is, we'll treat this as the first measurement (the 'a'). So we'll only have to do two more, but Lenny wants to simplify things, and do 'b' only for the first pair. Then, he'll prepare an identical quantum state with 'b' and measure 'c' (and as I said, that's really a repetition of the first measurement), and finally he'll do the 'ac' measurement.
We do measurements by entangling using a CNOT operator
\(U_1=|\theta_1\rangle \langle\theta_1|\otimes \mathbb{1} +|\bar\theta_1\rangle \langle\bar\theta_1|\otimes\sigma_x\;.\)
Here, \(|\theta_1\rangle \langle\theta_1|\) is the projector into the new basis, and \(|\bar\theta_1\rangle \langle\bar\theta_1|=1-|\theta_1\rangle \langle\theta_1|\) is the projector on the orthogonal basis state. \(\sigma_x\) is the first Pauli matrix, and just flips a qubit.
Here's a little exercise for you: you can write the same operator as
\(U_1=e^{i\pi/2 |\theta_1\rangle \langle\theta_1|\otimes \sigma_y}\;.\)
We won't do this exercise here. But if this is stunning to you, go ahead and expand the exponential and so forth, it'll be worth it. And no, it's not a typo in the exponent: it is really the y-Pauli matrix.
The angle \(\pi/2\) in the above expression is the "flipping" part of the operator. In a weak measurement, we just use a smaller angle \(\phi\) instead. If you do that, then instead of moving your ancilla from \(|0\rangle\) to \(|1\rangle\), you instead movie it to the state
\(|\epsilon\rangle=\sqrt{1-\epsilon^2}|0\rangle + \epsilon|1\rangle\;.\)
Oh, and \(\cos(\phi)=\sqrt{1-\epsilon^2}\). So basically, we now repeat the entire calculation with a weak measurement
\(U_1=e^{i\phi |\theta_1\rangle \langle\theta_1|\otimes \sigma_y}\;,\)
keeping in mind that in the limit \(\phi\to\pi/2\) we return to a strong measurement, but in the limit of \(\phi\to0\) the measurement becomes so weak that it does not even take place! Just what we need!
Alright, here's the plan. We still measure the quantum state with the 'a' measurement in whatever basis. The next measurement is the middle one, so it needs to be potentially weak, so we perform it with a strength \(\phi\), at angle \(\theta\). Just to be clear: \(\phi\) is the strength of measurement, with 0 meaning no measurement, and \(\pi/2\) meaning full-strength orthogonal measurement. The angle is still \(\theta\). The last measurement will be strong again, at angle \(\theta\) again. The calculation for the correlation function now gives
\(K_{12}=(1-\epsilon^2) + \epsilon^2\cos(\theta)\)
and you're not surprised to recover \(K_{12}=\cos(\theta)\) when the weak measurement is strong instead. Now let's calculate
\(K_{23}=(1-\epsilon^2)\cos^2(\theta) + \epsilon^2\cos(\theta)\;.\)
You can check again that in the limit \(\epsilon\to1\) you recover the old (strong) result. Finally,
\(K_{13}\) does not depend on \(\epsilon\) because it is the 'ac' measurement and only 'b' is potentially weak. (Not that this is only true if the first measurement prepares the quantum state in an eigenstate, as opposed to a superposition, of the first detector basis.)
Let's write down the Leggett-Garg inequality for this generalized (weak) 'b' measurement:
\(K_{12}+K_{23}-K_{13}=1-\epsilon^2(1-\cos(\theta))^2\;.\)
In the limit of a non-existing measurement 'b' \(\epsilon\to0\), we get
\(K_{12}+K_{23}-K_{13}=1\;\)
the same result we obtained when we didn't do the second measurement by choosing the first \(\theta=0\). Whichever way we choose not to do the middle measurement (because we want to simplify our work by doing only pairs of measurements), the Leggett-Garg inequalities cannot be violated. Ever.
What does all this mean for us? Well, people have wondered over and over again why it is so easy to violate inequalities that should be observed by quantum mechanics. Some (including Leggett) have suggested that when it comes to macroscopic phenomena, quantum mechanics can't be the right theory. Of course, you might say, we use classical mechanics there. But you need to remember that classical mechanics is not a correct theory. We need to be able to describe classical objects with quantum mechanics, or at least something that both describes microscopic and macroscopic objects accurately at the same time. Others have suggested that quantum mechanics is indeed the right theory, but that we just haven't (for a variety of reasons) been able to observe the deviations that the violation of LG inequalities implies. One of the reasons suggested by that camp is that perhaps we can never really perform perfectly strong measurements, and that this ``fuzziness" of measurements might obscure the violations [2]. Instead, we now realize that there are no paradoxes at all. Quantum mechanics correctly describes both microscopic and macroscopic physics. And we see no "weird" stuff in quantum measurement of macroscopic devices not because strong measurements can't be achieved, but because those violations simply do not exist. They are based on the faulty thinking that plagued Lenny. I do realize that there are literally hundreds of papers that follow Lenny's thinking in making pairwise experiments. All of them claim the Leggett-Garg inequalities are violated. All of them are wrong.
The preprint describing this work is [3] below. I have applied this thinking to the so-called "entropic" Leggett-Garg inequalities, which are related to the original inequalities but distinct. In [4] I show that these can't be violated either.
[1] A. J. Leggett and A. Garg, “Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks?” Phys. Rev. Lett. 54, 857–860 (1985).
[2] J. Kofler and C. Brukner, “Conditions for quantum violation of macroscopic realism,” Phys. Rev. Lett. 101, 090403 (2008).
[3] C. Adami, “Leggett-Garg inequalities cannot be violated in quantum measurements,” arXiv:1908.02866 (2019)
[4] C. Adami, “Neither weak nor strong entropic Leggett-Garg inequalities can be violated,” arXiv:1908.03124 (2019).




No comments:
Post a Comment