The year 2015 may go down in history for a lot of things. Just this December saw a number of firsts: A movie about armed conflict among celestial bodies breaks all records, a rocket delivers a payload of satellites and returns back to Earth vertically, not to mention the politics of the election cycle. But just maybe, 2015 will also be remembered as the year that people started warning about the dangers of Artificial Intelligence (AI). In fact, none other than Elon Musk, the founder of SpaceX who accomplished the improbable feat of landing a rocket, is one of the more prominent voices warning of AI. After giving $10 million to the "Future of Life" Institute (whose mission is "safeguarding life and developing optimistic visions of the future", but mostly warns about the dangers of AI), he co-founded OpenAI, a non-profit research company that aims to promote and develop open-source "friendly AI".
I wrote about my thoughts on this issue--that is, the dangers of AI--in a piece for the Huffington Post that you can read here. The synopsis (for those of you on a tight reading schedule) is that while I think that it is a reasonable thing to worry about such questions, the fears of a rising army of killing robots are almost certainly naive. The gist is that we are nowhere near creating the kind of intelligence that we should be afraid of. We cannot even design the intelligence displayed by small rodents, let alone creatures that think and plan our demise.
When discussing AI, I often make the distinction between "Type I" and "Type 2" intelligence. "Type I" is the kind we are good at designing today: the Roomba, Deep Blue, Watson, and the algorithm driving the Google self-driving car. Even the Deep Neural Nets that have been one of the harbingers, it seems, of the newfound fears, squarely belong into this group. These machine intelligences are of Type I (those that you do not need to fear), because they aren't really intelligent. They don't actually have any concept of what it is they are doing: they are reacting appropriately to the input they are presented with. You know not to fear them, because you will not worry about Deep Blue driving Google's car, or Jeopardy-beating Watson to recognize cat videos on the internet.
Type 2 intelligence is different. Type 2 has representations about the world in which it exists, and uses these representations (abstractions, toy models) to make decisions, plans, and to think about thinking. I have written about the importance of representations in another blog post, so I won't repeat this here.
If you could design Type 2 intelligence, I would be scared too. But you can't. That is, essentially, my point when I tell people that their fears are naive. The reasons for the failure of the design approach are complex, and detailed in another blog post. You want a synopsis of that one too? Fine, here it is: That stuff ain't modular, and we can only design modular stuff. Type 2 intelligence integrates information at an unheard-off level, and this kind of non-modular integration is beyond our design capabilities, perhaps forever.
I advocate that you cannot design Type 2 intelligence, but you can evolve it. After all, it worked once, didn't it? And that is what my lab (as well as Jeff Clune's lab and now Arend Hintze's lab also) is trying to achieve.
I know, I know. You are asking: "Why do you think that evolving AI should be less dangerous than designed AI?" This is precisely the question I will try to answer in this post. Along the way, I will shamelessly plug a recent publication where we introduce a new tool that will help us achieve the goal. The goal that we all are looking for--some with trepidation, some with determination and conviction.
The answer to this question lies in the "How" of the evolutionary approach. To those not already familiar with the evolutionary approach (if this is you: my hat off to you for reading this far), this approach is firmly rooted in emulating the Darwinian process that has given rise to all the biological complexity you can see on our planet. The emulation is called the "Genetic Algorithm".
Here's the "Genetic Algorithm" (GA, for short) for you in a nutshell. Mind you, a nutshell is only large enough to hold but the most basic of stuff about GAs. But here we go. In a GA, a population of candidate "solutions" to a given problem is maintained. The candidates encode the solution in terms of symbolic strings (often called "genotypes"). The strings encode the solution in a way so that small changes to the string give rise to small changes to the solution (mostly). Changes (called mutations) are made to the genotypes randomly, and often strings are recombined by taking pieces of two different strings and merging them. After all the changes are done, the sequences in the new population are tested, and each has a fitness assigned to them. Those with high fitness are given relatively more offspring to place into the next generation, and those with less fitness ... well, less so. Because those types with "good genes" get more representation in the next generation (and those with bad genes barely leave any) over time fitness increases, and complex stuff ensues.
Clearly (we can all attest to that), this is some powerful algorithm. You would not be here reading this without it, because it is the algorithm behind Darwinian evolution, which made you. But as powerful as it is, it also has an Achilles heel. The algorithm preferentially selects types that have higher fitness than the prevailing type. That's the whole point, of course, but what if the highest type is far away, and the path towards it must go through less fit types? In that case, the preference for fitter things is actually an impediment, because you can't tell the algorithm to "stop wanting higher fitness for a little while".
This problem is known as the "valley-crossing" problem. Consider the fitness landscape in the figure below.
This is known as a "rugged" fitness landscape (for obvious reasons). You are to think of the x and y coordinates of this picture as the genotype, and the z-axis as the fitness of that type. Of course, in realistic landscapes the type is specified by far more than two numbers, but it would not be as easily depicted. Think of the x and y coordinates as the most important numbers to characterize the type. In evolutionary biology, such "important characters" are called "traits".
If a population occupies one of these peaks, an evolutionary process will have a hard time to make it to another (higher) peak, as the series of changes that the type has to undergo to move to the new peak must lead through valleys. While it is in a valley, it is outcompeted by those types that are not attempting the "trip" to higher ground. Those types that are left behind and stick to the "old ways" of doing things, they are like reactionaries actively opposing progress. And in evolution, these forces are very strong.
What can you do to help the evolutionary algorithm see that it is OK to creep along at lower fitness for a little while? There are in fact many things that can be done, and there are literally hundreds, if not thousands of papers that have been written to address this problem, both in the world of evolutionary computation and in evolutionary biology. It is one of the hottest research fields in evolution.
I cannot here describe the different approaches that have been taken to increase evolvability in the computational realm, or to understand evolvability in the biological realm. There are books about this topic. I will describe here one way to address this problem, in the context of our attempts to evolve intelligent behavior. The trick is to exploit the fact that the landscape really has many more dimensions than the one you are either visualizing, or even the one you are using to calculate the fitness. Let me explain.
In evolutionary computation, you generally specify a way to calculate fitness from the genotype. This could be as simple as "count the number of 1s in the binary string". Such a fitness landscape is simple, non-deceptive (because all paths that lead upwards actually lead to the highest peak) and smooth (there is only one peak). Evolution stops once the string "1111...1111" is found. In the evolution of intelligence, it takes much more to calculate fitness. This is because the sequence, when interpreted, literally makes a brain. That brain must then be loaded onto an agent, who then has to "do stuff" in its simulated world. The better it "does stuff", the higher its score. The higher its score, the higher its fitness. The higher its fitness, the more offspring it will leave in the next generation. And because the offspring inherit the type, the more types in the next generation that can "do stuff". Which is a good thing, as now each one of those has a chance to find out (I mean, via mutations) how to "do even more stuff".
In one of the examples of the paper that I'm actually blogging about the agent has to catch some types of blocks that are raining down, and avoid others. Here's a picture of what that world looks like:
The agent is the rectangular block on the bottom, and it can move left or right. It looks upwards using the four red triangles. Using these "eyes" it must determine whether the block raining down (diagonally, either left or right) is small or large. It it is small it should catch it, but if it is large it should avoid it. The problem is, the agent's vision is poor: it has a big blind spot between the sensors, so a small and a large block may look exactly the same, unless you move around, that is. That is why this classic task is called "active categorical perception": in order to perceive and classify the shape (which you do by either catching or avoiding), you have to move actively.
This is a difficult problem for the agent, as it takes a little while to determine what the object even is. Once you know what it is, you have to plan your move in such a way that the object will touch you (if it is small) or not touch you (if it is large). This means that you have to predict where it is going to land, and make your moves accordingly. And all that before the brick has hit the floor. You do need memory to pull this off, as without it you will not be able to determine the trajectory.
We have previously shown that you can evolve brains that can do this task perfectly. But this does not mean that every evolutionary trajectory reaches that point. Quite to the contrary: most of the time you get stuck at these intermediate peaks of decent, but not perfect, performance. We looked for ways to increase those odds, and here's what we came up with. What you want to do is reward things other than the actual performance. Things that you think might make a better brain, but that might not, just at this moment, make you better at the block-catching task. We call these things "neuro-correlates": characters that are correlated with good neurological processing in general. It is like selecting for good math ability when the task at hand is survival from being hunted by predators. Being good at math may not save you right then and there (while being fast would), but in the long run, being good at math will be huge because for example you can calculate the odds of any evasion strategy, and thus select the right one. Math could help you in a myriad of ways. Later on, in another hunt.
After all, the problem with the evolutionary algorithm is its short-sightedness: it cannot "see" the far-off peaks. Selecting for traits that you, the investigator, trust are "good for thinking in general" (the neuro-correlates) is like correcting for the short-sightedness of evolution. The mutations that increase the neuro-correlate traits would ordinarily not be rewarded (until they become important later on). By rewarding them early, you may be able to jump start evolution.
So that is what we tried, in the paper that I'm blogging about, and that appeared on Christmas Day 2015. We tried a litany of neuro-correlates (eight, to be exact). The neuro-correlates that we tested can roughly be divided into two categories: network-theory based, and information-theory based. Since the Markov brains that we evolve are networks of neurons, network-theory based measures make sense. As brains also process information, we should test information-processing measures as well.
The network-based measures are mostly your usual suspects: density of connection (in the expert parlance: mean degree), sparsity, length of longest shortest path, and a not so obvious one: length of genome encoding the network. The information-theoretic ones are perhaps less obvious: we chose information integration, representation, and two types of predictive information. If I would attempt to describe these measures in detail (and why we chose them) I might as well repeat the paper. For the present purpose, let's just assume that they are well defined, and that they may or may not aid evolution.
Which is exactly what we found empirically. Suppose, for example, that you reward (aside from rewarding the catching of the blocks) a measure that quantifies how well you integrate information. There is indeed such a measure: it is called $\Phi$ (Phi), and I blogged about that before. You can imagine that information integration might be important for this task: the agent has to integrate the visual information from different time points along with other memories to make the decision. So the trick is that any mutation that increases information integration will have an increased chance of making it into the next generation, even though it may not be useful at that moment. So, in other words, we are helping evolution to look forward in time, by keeping certain mutations around even if they are not useful at the time that they occur. Doing this, what may have looked like a valley in the future, may not be a valley after all (because of the presence of a mutation that was integrated into the genome ahead of time).
So what should we reward? Easy, right? Reward those mutations that help the brain work well! Oh wait, we don't know how the brain works. So, we have to make guesses as to what things might make the brain work well. And then test which of these, as a matter of fact, do help in hindsight. Here are the eight that we tested:
Network-theory based:
1. Minimum Description Length (MDL) (which here you can think of as a proxy for "brain size")
2. Graph Diameter (Longest of all shortest paths between node pairs)
3. Connectivity (the mean degree per node)
4. Sparseness (kind of the opposite of connectivity)
Information-theory based:
5. Representation (having internal models of the world)
6. Information Integration (Phi, the "atomic variant")
7. Predictive information (between sensor states)
8. Predictive Information (between sensor and actuator states)
Here's what we found: Graph diameter, Phi, and connectivity all three significantly help the evolutionary algorithm when the overall rewarded function is the fitness times the neuro-correlate. Sparseness, as well as the two predictive information measures, made things worse. This finding reinforces the suspicion that we really don't know what makes brains work well. In neuroscience, sparse coding is considered a cornerstone of neural coding theory, after all. But we should keep in mind that these findings can very well depend significantly on the type of task investigated, and that for other tasks the findings for what works might be reversed. For example, the block-catching task requires memory, and predictive information is maximized for purely reactive machines. If the task did not require memory, it is likely that predictive information is a good neuro-correlate.
To check how much the value of the neuro-correlate depends on the task chosen, we repeated the entire analysis for a very different task: one that does not even require the agent to have a body.
The alternate task we tested is the ability to generate random numbers using only deterministic rules. That this is a cognitively complex task has been known for some time: the ability to generate random (or, I should say, random-ish) numbers is often used to assess cognitive deficiencies in people. Indeed, if you (a person) were asked to do this, you would need to keep track of not only the last 5-7 numbers you generated (which you can do using short-term memory), but also of how often you have produced doubles, and triples, etc, and of what numbers. The more you think about this task, you appreciate its complexity. And you can easily imagine that different cognitive impairments might lead to different signature departures from randomness.
Of course this task is easy if you have access to a random number generator. but the Markov brains had none. So they had to figure out an algorithm to produce the numbers (which is also what we do in computers to produce pseudo-random numbers).
The results with the random number generation (RNG) task were roughly the same as with the block-catching task: Graph diameter, Phi, and connectivity scored well, while predictive information and sparseness scored negatively. Representation cannot be used as a neuro-correlate for this task, as there is no external world that the brain can create representations of. So while the individual results differ somewhat, there seems to be some universality in the results we found.
Of course, there are very likely better neuro-correlates out there that can boost the performance of the evolutionary algorithm much more. We don't know what these are, as we don't know what it is that makes brains work better. There are many suggestions, and we hope to try some in the future. We can think of
1. Other graph-based measures such as modularity
2. novelty search (rewarding brains that see or do things they haven't seen or done before)
3. conditional mutual information over different time intervals
4. Measures of information transfer
5. Dual total correlation
Of course, the list is endless. It is our intuition about what matters in computation in the brain that should guide our search for measures, and whether or not they matter is then found empirically. In this manner, evolutionary algorithms might also give us a clue about how all brains work, not just those in silico.
But I have not yet answered the question that I posed at the very beginning of this post. Most of you are forgiven for forgetting it as it is figuratively eons ago (or 36 paragraphs, which in blogging land is considered almost synonymous with eons). The straw man reader asked: "What makes you think that evolution (as opposed to design) will produce "nice" intelligences, that is, the kind that will not be bent on destruction of all of humanity?"
The answer is that we cannot (we firmly believe that) evolve intelligence in a vacuum. The world in which intelligence evolves must be complex, and difficult to predict. Thus, it must change in subtle ways, ways that takes intelligence to forecast. The best world to achieve this is a world in which there are other agents, with complex brains. Then, prediction requires the prediction of behaviors of others, which is best achieved by understanding the other. Perhaps, by realizing that the other thinks like you think. When doing this, you generally also evolve empathy. In other words, as we evolve our agents to survive in groups of other agents, cooperative behavior should ultimately evolve at the same time.
Our robots, when they first open their eyes to the real world, will already know what cooperation and empathy are. These are not traits that human programmers are thinking of, but evolution has stumbled upon these adaptive traits over and over again. That is why we are optimistic: we will be evolving robots with empathic brains. And if they show signs of psychopathology in their adolescence? Well, we know where the off switch is.
The publication this blog post is based on is open access (gold):
J. Schossau, C. Adami, and A. Hintze, Information-Theoretic Neuro-Correlates Boost Evolution of Cognitive Systems. Entropy 18 (2016) e18010006.
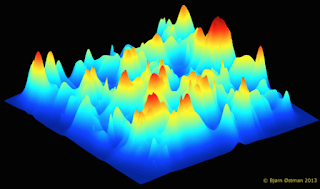 |
| A schematic fitness landscape where elevation is synonymous with fitness. Credit: Bjørn Østman. |
If a population occupies one of these peaks, an evolutionary process will have a hard time to make it to another (higher) peak, as the series of changes that the type has to undergo to move to the new peak must lead through valleys. While it is in a valley, it is outcompeted by those types that are not attempting the "trip" to higher ground. Those types that are left behind and stick to the "old ways" of doing things, they are like reactionaries actively opposing progress. And in evolution, these forces are very strong.
What can you do to help the evolutionary algorithm see that it is OK to creep along at lower fitness for a little while? There are in fact many things that can be done, and there are literally hundreds, if not thousands of papers that have been written to address this problem, both in the world of evolutionary computation and in evolutionary biology. It is one of the hottest research fields in evolution.
I cannot here describe the different approaches that have been taken to increase evolvability in the computational realm, or to understand evolvability in the biological realm. There are books about this topic. I will describe here one way to address this problem, in the context of our attempts to evolve intelligent behavior. The trick is to exploit the fact that the landscape really has many more dimensions than the one you are either visualizing, or even the one you are using to calculate the fitness. Let me explain.
In evolutionary computation, you generally specify a way to calculate fitness from the genotype. This could be as simple as "count the number of 1s in the binary string". Such a fitness landscape is simple, non-deceptive (because all paths that lead upwards actually lead to the highest peak) and smooth (there is only one peak). Evolution stops once the string "1111...1111" is found. In the evolution of intelligence, it takes much more to calculate fitness. This is because the sequence, when interpreted, literally makes a brain. That brain must then be loaded onto an agent, who then has to "do stuff" in its simulated world. The better it "does stuff", the higher its score. The higher its score, the higher its fitness. The higher its fitness, the more offspring it will leave in the next generation. And because the offspring inherit the type, the more types in the next generation that can "do stuff". Which is a good thing, as now each one of those has a chance to find out (I mean, via mutations) how to "do even more stuff".
In one of the examples of the paper that I'm actually blogging about the agent has to catch some types of blocks that are raining down, and avoid others. Here's a picture of what that world looks like:
 |
| The agent's world. Credit: the authors. |
This is a difficult problem for the agent, as it takes a little while to determine what the object even is. Once you know what it is, you have to plan your move in such a way that the object will touch you (if it is small) or not touch you (if it is large). This means that you have to predict where it is going to land, and make your moves accordingly. And all that before the brick has hit the floor. You do need memory to pull this off, as without it you will not be able to determine the trajectory.
We have previously shown that you can evolve brains that can do this task perfectly. But this does not mean that every evolutionary trajectory reaches that point. Quite to the contrary: most of the time you get stuck at these intermediate peaks of decent, but not perfect, performance. We looked for ways to increase those odds, and here's what we came up with. What you want to do is reward things other than the actual performance. Things that you think might make a better brain, but that might not, just at this moment, make you better at the block-catching task. We call these things "neuro-correlates": characters that are correlated with good neurological processing in general. It is like selecting for good math ability when the task at hand is survival from being hunted by predators. Being good at math may not save you right then and there (while being fast would), but in the long run, being good at math will be huge because for example you can calculate the odds of any evasion strategy, and thus select the right one. Math could help you in a myriad of ways. Later on, in another hunt.
After all, the problem with the evolutionary algorithm is its short-sightedness: it cannot "see" the far-off peaks. Selecting for traits that you, the investigator, trust are "good for thinking in general" (the neuro-correlates) is like correcting for the short-sightedness of evolution. The mutations that increase the neuro-correlate traits would ordinarily not be rewarded (until they become important later on). By rewarding them early, you may be able to jump start evolution.
So that is what we tried, in the paper that I'm blogging about, and that appeared on Christmas Day 2015. We tried a litany of neuro-correlates (eight, to be exact). The neuro-correlates that we tested can roughly be divided into two categories: network-theory based, and information-theory based. Since the Markov brains that we evolve are networks of neurons, network-theory based measures make sense. As brains also process information, we should test information-processing measures as well.
The network-based measures are mostly your usual suspects: density of connection (in the expert parlance: mean degree), sparsity, length of longest shortest path, and a not so obvious one: length of genome encoding the network. The information-theoretic ones are perhaps less obvious: we chose information integration, representation, and two types of predictive information. If I would attempt to describe these measures in detail (and why we chose them) I might as well repeat the paper. For the present purpose, let's just assume that they are well defined, and that they may or may not aid evolution.
Which is exactly what we found empirically. Suppose, for example, that you reward (aside from rewarding the catching of the blocks) a measure that quantifies how well you integrate information. There is indeed such a measure: it is called $\Phi$ (Phi), and I blogged about that before. You can imagine that information integration might be important for this task: the agent has to integrate the visual information from different time points along with other memories to make the decision. So the trick is that any mutation that increases information integration will have an increased chance of making it into the next generation, even though it may not be useful at that moment. So, in other words, we are helping evolution to look forward in time, by keeping certain mutations around even if they are not useful at the time that they occur. Doing this, what may have looked like a valley in the future, may not be a valley after all (because of the presence of a mutation that was integrated into the genome ahead of time).
So what should we reward? Easy, right? Reward those mutations that help the brain work well! Oh wait, we don't know how the brain works. So, we have to make guesses as to what things might make the brain work well. And then test which of these, as a matter of fact, do help in hindsight. Here are the eight that we tested:
Network-theory based:
1. Minimum Description Length (MDL) (which here you can think of as a proxy for "brain size")
2. Graph Diameter (Longest of all shortest paths between node pairs)
3. Connectivity (the mean degree per node)
4. Sparseness (kind of the opposite of connectivity)
Information-theory based:
5. Representation (having internal models of the world)
6. Information Integration (Phi, the "atomic variant")
7. Predictive information (between sensor states)
8. Predictive Information (between sensor and actuator states)
Here's what we found: Graph diameter, Phi, and connectivity all three significantly help the evolutionary algorithm when the overall rewarded function is the fitness times the neuro-correlate. Sparseness, as well as the two predictive information measures, made things worse. This finding reinforces the suspicion that we really don't know what makes brains work well. In neuroscience, sparse coding is considered a cornerstone of neural coding theory, after all. But we should keep in mind that these findings can very well depend significantly on the type of task investigated, and that for other tasks the findings for what works might be reversed. For example, the block-catching task requires memory, and predictive information is maximized for purely reactive machines. If the task did not require memory, it is likely that predictive information is a good neuro-correlate.
To check how much the value of the neuro-correlate depends on the task chosen, we repeated the entire analysis for a very different task: one that does not even require the agent to have a body.
The alternate task we tested is the ability to generate random numbers using only deterministic rules. That this is a cognitively complex task has been known for some time: the ability to generate random (or, I should say, random-ish) numbers is often used to assess cognitive deficiencies in people. Indeed, if you (a person) were asked to do this, you would need to keep track of not only the last 5-7 numbers you generated (which you can do using short-term memory), but also of how often you have produced doubles, and triples, etc, and of what numbers. The more you think about this task, you appreciate its complexity. And you can easily imagine that different cognitive impairments might lead to different signature departures from randomness.
Of course this task is easy if you have access to a random number generator. but the Markov brains had none. So they had to figure out an algorithm to produce the numbers (which is also what we do in computers to produce pseudo-random numbers).
The results with the random number generation (RNG) task were roughly the same as with the block-catching task: Graph diameter, Phi, and connectivity scored well, while predictive information and sparseness scored negatively. Representation cannot be used as a neuro-correlate for this task, as there is no external world that the brain can create representations of. So while the individual results differ somewhat, there seems to be some universality in the results we found.
Of course, there are very likely better neuro-correlates out there that can boost the performance of the evolutionary algorithm much more. We don't know what these are, as we don't know what it is that makes brains work better. There are many suggestions, and we hope to try some in the future. We can think of
1. Other graph-based measures such as modularity
2. novelty search (rewarding brains that see or do things they haven't seen or done before)
3. conditional mutual information over different time intervals
4. Measures of information transfer
5. Dual total correlation
Of course, the list is endless. It is our intuition about what matters in computation in the brain that should guide our search for measures, and whether or not they matter is then found empirically. In this manner, evolutionary algorithms might also give us a clue about how all brains work, not just those in silico.
But I have not yet answered the question that I posed at the very beginning of this post. Most of you are forgiven for forgetting it as it is figuratively eons ago (or 36 paragraphs, which in blogging land is considered almost synonymous with eons). The straw man reader asked: "What makes you think that evolution (as opposed to design) will produce "nice" intelligences, that is, the kind that will not be bent on destruction of all of humanity?"
The answer is that we cannot (we firmly believe that) evolve intelligence in a vacuum. The world in which intelligence evolves must be complex, and difficult to predict. Thus, it must change in subtle ways, ways that takes intelligence to forecast. The best world to achieve this is a world in which there are other agents, with complex brains. Then, prediction requires the prediction of behaviors of others, which is best achieved by understanding the other. Perhaps, by realizing that the other thinks like you think. When doing this, you generally also evolve empathy. In other words, as we evolve our agents to survive in groups of other agents, cooperative behavior should ultimately evolve at the same time.
Our robots, when they first open their eyes to the real world, will already know what cooperation and empathy are. These are not traits that human programmers are thinking of, but evolution has stumbled upon these adaptive traits over and over again. That is why we are optimistic: we will be evolving robots with empathic brains. And if they show signs of psychopathology in their adolescence? Well, we know where the off switch is.
The publication this blog post is based on is open access (gold):
J. Schossau, C. Adami, and A. Hintze, Information-Theoretic Neuro-Correlates Boost Evolution of Cognitive Systems. Entropy 18 (2016) e18010006.