Here's to you, quantum measurement afficionado, who has found their way to the sixth installment, breathless (I hope), to learn of the fate of the famous cat, eponymous with one of the great ones of quantum mechanics. Does she live or die? Can she be both dead and alive? What did this kitten ever do to deserve such an ambiguous fate? And, how many times can you write a blog post teasing cat-revelations and still not talk about it after all? And talk about erasers instead? How many?
In my defense, I tried to talk about the cat in this post. I really did. But the quantum eraser, and in particular the double-slit experiment that I have to describe first, took so much room that it was just not in the cards. But rejoice then, this series will be even longer!
<Silence>
OK then. I think we are beyond the obligatory summary of previous posts now. This can get tedious very fast. ("In Part 27, we learned that,..."). Instead, I refer those who stumbled on this, to peruse the first post here, which should be enough to get you on the road.
So where were we? In the last post, I ended with teasing you with the quantum eraser. This post will all be about the quantum description of these seemingly paradoxical situations: the two-slit experiment, and the quantum eraser. Post 7 will be thus be the one concerned with Felis Schröderingii, and it is Part 8 that will deal with even more obscure paradoxes such as the Zeno and Anti-Zeno effect. But that post will use these paradoxes as a ploy to investigate something altogether more important: namely the legacy of Hans Bethe's insight from the very first post of the series.
Foreshadowing aside, let's take a look at the infamous double-slit experiment (also know as "Young's experiment"). Richard Feynman (in his lectures) famously remarked that the experiment is "a phenomenon which is impossible […] to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery.
Really, the only mystery?
Well, once I get through all this (meaning this and the following posts), you might agree that perhaps this is not so far off the mark. If I can get you to slowly and knowingly nod about this statement (while thinking thet there is also much more to QM than that), then I did my job.
As is my want, I will be borrowing images from Wikimedia to illustrate stuff. (Because they explicitly encourage that sort of thing). Here, for example, is what they would show about the double-slit experiment:
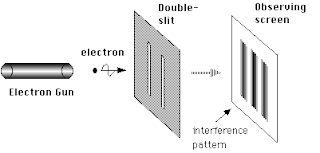 |
| Fig. 1: The double-slit experiment (source: Wikimedia) |
Here's what happens in this experiment. You shoot electrons at a screen that has, yes you guessed it, two slits. It is important that these are electrons, not photons. (Actually it is not but you would not understand why I say this just yet. So let's forget I even uttered this). You shoot particles at a screen. Particles! (Imagine this in the voice of Seinfeld's Seinfeld). There is a screen behind the double slit. It records where the electrons that got through the slits land. What would you expect to find there?
Maybe something like this?
 |
| Fig. 2: The pattern expected at the screen if classical particles are sent in from the left. |
If the world was classical, yes this is what you would see. But the world is not classical, and this is not what we observe. What you get (and what you are looking at below is data from an actual such experiment) is this:
 |
| Fig. 3: The intensity pattern on the screen if quantum particles are sent in. (Source: Wikimedia) |
Now, don't focus on the fact that you have a big blob in the middle, and two smaller blobs left and right. I don't have time (and neither do you) to explain those. Focus on the blob in the middle instead. You thought you were going to see two intense blobs of light, one behind each slit. But you don't. You think something is wrong with your apparatus. But try as you might, you get this pattern every time.
What you should focus on are the dark lines that interrupt the blob. Where on earth do they come from? They look suspiciously like interference patterns, as if you had shone some light on the double slit, like so:
 |
| Fig. 3: Interference patterns from light shining on a double slit. |
But you did not shine light on these slits. You sent particles. Particles! A particle cannot interfere with itself! Can it?
Here is where we pause. You certainly have to hand it to Feynman. It seems these electrons are not your ordinary classical particles.
The pattern on the screen does not tell you that an electron "went through one or the other slit". The electron's wavefunction interacts with the slits, and then the entangled wavefunction interacts with the screen, and then you look at the screen (not the quantum state, as you remember). Lets find out how that works, using the formalism that we just learned. (Of course you saw this coming, didn't you?)
Say you have your electron, poised to be sent onto the double slit. It is described by a wave function \(\Psi(x)\). All your standard quantum stuff applies to this wavefunction by the way, such as an uncertainty relation for position and momentum. I could have written down the wavefunction of a wave packet traveling with momentum p just as well. None of these complications matter for what I'm doing here.
When this wavefunction crosses the double slit, it becomes a superposition of having gone through the slit L and through the slit R, and I can write it like this (see Figure below).
\(|\Psi_1\rangle=\frac1{\sqrt 2}\left(|\Psi_L\rangle+|\Psi_R\rangle\right)\). (1)
I have written \(|\Psi_1\rangle\) in terms of the "bra-ket" notation to remind you that the wavefunction is a vector, and I have identified only the position (because this is what we will measure later).
 |
| Fig. 4: Sketch of the double-slit experiment in terms of wavefunctions |
Of course, you are free to roll your eyes and say "How could the electron possibly be in a superposition of having gone through the left slit and the right slit at the same time?" But that is precisely what you have to assume in order to get the mathematics to agree with the experimental result, which is the intensity pattern on the right in the figure above.
What happens when we re-unite the two branches of the wavefunction at the spot where I write \(\Psi_2\) in the figure above and then measure the space-component of the wavefunction? We learned in Parts 1-5 how to make that measurement, so let's get cracking.
I spare you the part where I introduce the measurement device, entangle it with the quantum system, and then trace over the quantum system, because we already know what this gives rise to: Born's rule, which says that the likelihood to get a result at x is equal to the square of the wavefunction
\(P(x)=| \langle x|\Psi_2\rangle|^2=|\Psi_2(x)|^2\). (2)
There, that's how simple it is. I remind you here that you can use the square of the wavefunction instead of the square of the measurement device's likelihood because they are one and the same. The quantum entanglement tells you so. The Venn diagram tells you so. If this is not immediately obvious to you, I suggest a revisiting of Parts 4 & 5.
Let's calculate it then. Plugging (1) into (2) we get
We then get the entangled state:
\(|\Psi\rangle=\frac1{\sqrt2}\left(|\Psi_L\rangle|d\rangle+|\Psi_R\rangle |u\rangle\right)\) . (5)
If we put such a detector just before the screen (as in Fig. 7 below), the wavefunction becomes
\(\frac1{\sqrt2}\left(|\Psi_L\rangle|d\rangle+|\Psi_R\rangle |u\rangle\right)\rightarrow \frac1{2}\left(|\Psi_L\rangle|+|\Psi_R\rangle\right)\frac1{\sqrt2}(|u\rangle+|d\rangle)\), (7)
that is, the space wavefunction and the spin wavefunction are disentangled; they are back to being a product. You lose half your initial amplitude, yes. (See the factor 1/2 in (7)?)
Part 7 is here. Sorry, no cats.
[1] M.O. Scully and K. Drühl, Quantum eraser – a proposed photon-correlation experiment concerning observation and delayed choice in quantum mechanics, Phys. Rev. A 25, 2208 (1982).
[2] M.O. Scully, B.-G. Englert, H. Walther, Quantum optical tests of complementarity, Nature 351, 111 (1991).
[3] S. P. Walborn, M. O. Terra Cunha, S. Padua, Double-slit quantum eraser. Phys. Rev. A 65, 033818 (2002).
\(P(x)=\frac12\left(|\Psi_L(x)|^2+|\Psi_R(x)|^2+ 2 {\rm Re}[\Psi_L^\star(x)\Psi_R(x)]\right)\) (3)
The two first terms in (3) do what you are used to in classical physics: they make a smudge on the screen at the locations of the two slits, \(x=L\) and \(x=R\). The interesting part is the third term, which is given by the real part of the product of the complex conjugate of \(\Psi_L(x)\) with \(\Psi_R(x)\). That's what the math says. And if you write down what these things are, you will find that these are the parts that create the "fringes", namely the interference pattern between \(\Psi_L\) and \(\Psi_R\). That's because that cross term can become negative, while the first two terms must be positive. If you did not have a wavefunction split just like I showed in (1), then you would not get that cross term, and you would not be able to understand the experiment. And hence you would not understand how the world works.
"But, but.." I can almost here some of you object, "surely I can find out through which of the slits the electron actually went, no?"
Indeed you could try. Let's see what happens if you do. One way to do this is to put a device into the path of the electron that flips its spin (its helicity) in one of the branches (say the left, L), but not in the right. Then all I had to do is measure the helicity to know through which it went, right? But how would you explain, then, the interference pattern?
Well, let's try this (and ignore for a moment that this experiment is not at all easy to do with electrons (but it is very easy to do with photons, and using polarization instead of helicity). So now the wavefunction has another tag, which I will call u (for "up" so I don't have to type \(\uparrow\) all the time), and d.
After the slits, the wave funtion becomes
\(|\Psi_1\rangle=\frac1{\sqrt2}(|\Psi_L\rangle|u\rangle+|\Psi_R\rangle|u\rangle) \) (4)
The new identifier ("quantum number") is in a product state with respect to all the other quantum numbers. And if nothing else happened, these quantum numbers would not affect the interference patters. (This is why I was able to ignore the momentum variable above, for example: it is in a product state). But now let's put the helicity flipper into the left pathway, like in the figure below:
 |
| Fig. 6: Double-slit interference experiments with location variable tagged by helicity |
\(|\Psi\rangle=\frac1{\sqrt2}\left(|\Psi_L\rangle|d\rangle+|\Psi_R\rangle |u\rangle\right)\) . (5)
All right, you managed to tag the location variable with helicity. Now we could measure the helicity to find out which slit the electron went through, right? But before we do that, let's take a look at the interference pattern, by calculating \(P(x)\) as before. Rather than (3), we now get
\(\frac12\left(|\Psi_L(x)|^2\langle d|d\rangle +|\Psi_R(x)|^2\langle u|u\rangle
+ \Psi_L^\star(x)\Psi_R(x)\langle d|u\rangle + \Psi_R^\star(x)\Psi_L(x)\langle u|d\rangle\right)\)
+ \Psi_L^\star(x)\Psi_R(x)\langle d|u\rangle + \Psi_R^\star(x)\Psi_L(x)\langle u|d\rangle\right)\)
Now, the helicity states \(|u\rangle\) and \(|d\rangle|\) are orthogonal, of course. What that means is that \(\langle d|d\rangle=\langle u|u \rangle=1\) while \(\langle d|u\rangle=\langle u|d\rangle=0\), and \(P(x)\) simply becomes
\(P(x)=\frac12\left(|\Psi_L(x)|^2+|\Psi_R(x)|^2\right)\). (6)
and the interference term--is gone. What you get is the pattern that you see on the right hand side of the figure above: no fringes, just two peaks (one from the left slit, one from the right).
You note of course that we didn't even need to measure the helicity in order to destroy the pattern. Just making it possible to do so was sufficient.
But guess what. We can undo this attempt at a measurement. Yes, we can "unlook" the location of the electron, and get the interference pattern back. That's what the quantum eraser does, and you'd be surprised how easy it is.
The trick here is to insert a filter just before measuring the re-united wavefunction. This filter measures the wavefunction not in the orthogonal basis \((u,d)\) but rather in a basis that is rotated by 45\(^\circ\) with respect to the \((u,d)\) system. The rotated basis states are
\(|U\rangle=\frac1{\sqrt2}(|u\rangle+|d\rangle)\) and \(|D\rangle=\frac1{\sqrt2}(|u\rangle-|d\rangle)\). Detectors that measure in such a rotated (or "diagonal") basis are easy to make for photon polarizations, and quite a bit harder for spins, but let that be an experimental quibble.
If we put such a detector just before the screen (as in Fig. 7 below), the wavefunction becomes
\(\frac1{\sqrt2}\left(|\Psi_L\rangle|d\rangle+|\Psi_R\rangle |u\rangle\right)\rightarrow \frac1{2}\left(|\Psi_L\rangle|+|\Psi_R\rangle\right)\frac1{\sqrt2}(|u\rangle+|d\rangle)\), (7)
that is, the space wavefunction and the spin wavefunction are disentangled; they are back to being a product. You lose half your initial amplitude, yes. (See the factor 1/2 in (7)?)
 |
| Fig. 7: Double-slit experiment with eraser that reverses the previous measurement. The interference pattern re-emerges. |
How do you show that this is right? It's a simple application of the quantum measurement rules I showed you in Parts 1-5. To measure in the "diagonal" basis, you start with a measurement ancilla in one of the basis states (say \(|D\rangle\)), then write the L and R wavefunction in that basis, and then apply the measurement operators, which as you remember is the "attempted cloning" operator. Then finally you measure D (that is, you calculate \(\langle D|\Psi\rangle \)). I could show these three lines, or I could let you try them yourself.
I think I'll let you try it yourself, because you should really see how the disentanglement happens. Also, I'm really tired right now :-)
That this really could work was proposed first by Marlan Scully in the now classic experiment [1] (see also [2]). The experiment was carried out successfully multiple times, notably the experiment in [3]. You might object that they used photons and not electrons there. But the important point is the erasure of the which-path information provided by the "helicity-flipper" (which is a "polarization-rotator" if you're using photons), and that certainly does not depend on whether you are massive or not. Because you know, neither the photon nor the electron are particles. Because there is no such thing as a particle. There is only the illusion of particles generated by measurement devices that go 'click'. But if you have read this far, then you already know not to trust the measurement devices: they lie.
And the best illustration of these lies is perhaps Schrödinger's cat. You will get to play with the equations describing her, I promise. And maybe, just maybe, you will also come to appreciate that quantum reality, and the reality we perceive via our classical measurement devices, are two very different things.
Part 7 is here. Sorry, no cats.
[1] M.O. Scully and K. Drühl, Quantum eraser – a proposed photon-correlation experiment concerning observation and delayed choice in quantum mechanics, Phys. Rev. A 25, 2208 (1982).
[2] M.O. Scully, B.-G. Englert, H. Walther, Quantum optical tests of complementarity, Nature 351, 111 (1991).
[3] S. P. Walborn, M. O. Terra Cunha, S. Padua, Double-slit quantum eraser. Phys. Rev. A 65, 033818 (2002).

