Most textbooks tell you that the evolutionary process is really quite simple: three rules are all that's necessary: inheritance, variation, and selection. It is indeed true that these three rules are all that's needed for evolution to occur, but that does not mean that the evolutionary process is simple. In fact, quite the opposite. Real systems evolve in many different ways because the process takes place (is "instantiated") in many different environments. How the evolutionary process unfolds depends very much on those environments: they shape the mode and manner of adaptation.
Let me explain what I mean in more detail. How do the three necessary elements depend on the environment? The inheritance part of the "Darwinian Triad" isn't actually that susceptible to environmental variations (although there are cases). Variation (that is, changes incurred during transmission of genetic information from parent to child), and in particular selection, are very much subject to modulation by the environment. There are likely dozens of books written about the different ways that changes can occur to the carriers of information (yes, DNA) during replication, and this post won't be the one dwelling on those details. They are important, just not for this post. Here, we'll discuss the third pike of the Triad: selection.
It is very unlikely that you are reading this without being fairly well-versed in evolutionary biology, but just in case you got here from reading about black holes, here it is in a nutshell. Evolution occurs because random changes (variation) in the genetic information (that which is inherited) change the frequency at which that information is represented in a population, simply because the information is about how to make many copies of that information. Thus, information that is not increasing the fit of the organism to its environment tends to become less-represented, while information that leads to a better fit will increase in numbers, simply because a good fit means many copies. I realize that this may not be the way you have been taught the word "fitness" in the context of evolutionary biology in class, but it should have been.
Selection, by this account, really just means that "good info will be rewarded", in the sense that good info will increase the info-carrier's number of copies in the population. And because the world in which we (and this information) lives is finite, when one type gets to have more copies, there must be fewer of the less-fit types. As a consequence we will find that, over time, fitness along with the information on how to make a fit organism, increases over time on average. Most of the time.
Well yes, this law about the increase of information in evolution is not an absolute one. For example, because the information in your genome is about the world in which you live, it follows that when the world changes then some of what used to be information is ... not ... information anymore. And because information makes you fit, your fitness will almost always drop when the world has changed for you. But there are other cases where fitness can decrease in selection, and this post is about one of them.
There is a fairly classical (by now) case where lower fitness is actually selected for, and we need to talk about it briefly because it is relatively well-known and--it turns out--is somewhat of a bookend to the case I'll introduce you to shortly. This case is called the "Survival of the Flattest" effect (this is a pun meant to remind you that due to this effect, it is not the fittest that survives). Indeed, in this particular case fitness, measured in terms of the number of copies that the information--meaning the genome--can make, can drop in evolution. This happens if the mutation rate is very high, and there are fitness peaks that are not so very high, but kind of "flat" instead, so that mutated copies of the information are mostly still informative. In order not to make this post too long, I'l refer you to the Wiki page that describes this effect, and just show the video from that Wiki link that describes the effect, below.
Let me explain what I mean in more detail. How do the three necessary elements depend on the environment? The inheritance part of the "Darwinian Triad" isn't actually that susceptible to environmental variations (although there are cases). Variation (that is, changes incurred during transmission of genetic information from parent to child), and in particular selection, are very much subject to modulation by the environment. There are likely dozens of books written about the different ways that changes can occur to the carriers of information (yes, DNA) during replication, and this post won't be the one dwelling on those details. They are important, just not for this post. Here, we'll discuss the third pike of the Triad: selection.
It is very unlikely that you are reading this without being fairly well-versed in evolutionary biology, but just in case you got here from reading about black holes, here it is in a nutshell. Evolution occurs because random changes (variation) in the genetic information (that which is inherited) change the frequency at which that information is represented in a population, simply because the information is about how to make many copies of that information. Thus, information that is not increasing the fit of the organism to its environment tends to become less-represented, while information that leads to a better fit will increase in numbers, simply because a good fit means many copies. I realize that this may not be the way you have been taught the word "fitness" in the context of evolutionary biology in class, but it should have been.
Selection, by this account, really just means that "good info will be rewarded", in the sense that good info will increase the info-carrier's number of copies in the population. And because the world in which we (and this information) lives is finite, when one type gets to have more copies, there must be fewer of the less-fit types. As a consequence we will find that, over time, fitness along with the information on how to make a fit organism, increases over time on average. Most of the time.
Only most of the time?
Well yes, this law about the increase of information in evolution is not an absolute one. For example, because the information in your genome is about the world in which you live, it follows that when the world changes then some of what used to be information is ... not ... information anymore. And because information makes you fit, your fitness will almost always drop when the world has changed for you. But there are other cases where fitness can decrease in selection, and this post is about one of them.
There is a fairly classical (by now) case where lower fitness is actually selected for, and we need to talk about it briefly because it is relatively well-known and--it turns out--is somewhat of a bookend to the case I'll introduce you to shortly. This case is called the "Survival of the Flattest" effect (this is a pun meant to remind you that due to this effect, it is not the fittest that survives). Indeed, in this particular case fitness, measured in terms of the number of copies that the information--meaning the genome--can make, can drop in evolution. This happens if the mutation rate is very high, and there are fitness peaks that are not so very high, but kind of "flat" instead, so that mutated copies of the information are mostly still informative. In order not to make this post too long, I'l refer you to the Wiki page that describes this effect, and just show the video from that Wiki link that describes the effect, below.
The authors of this video were, incidentally, a grad student (Randy Olson) and a postdoc (Bjørn Østman) from my lab at Michigan State University at the time. And the not so humblebrag disclosure is that the effect was actually discovered in my lab at Caltech in 2001. You can read all about that by googling it.
But let's get back to the matter at hand. In "Survival-of-the-flattest", organisms that occupy flat (but not terribly high) fitness peaks can outcompete populations that live on high (and very pointy) peaks, but only when the mutation rate is high enough (see schematic drawing in the figure below).

Because of this "lower fitness outcompeting higher fitness" business, the effect violates the semi-edict of "ever-increasing information/fitness". It is a semi-law because, truthfully, nobody ever really declared it a law. It is a "most-of-the-time" law, much like the second law of thermodynamics, come to think of it.
The effect we'll discuss presently concerns population size rather than mutation rate, and just like the "survival-of-the-flattest" effect it violates the semi-edict; the almost-law. We shall call this new effect "survival-of-the-steepest". It goes without saying that this lame attempt at analogizing with the survival-of-the-flattest moniker couldn't be more obvious. But since that original moniker was due to Rich Lenski, and he did not object to this particular use, we'll just run with it and see if it sticks. (It may not.)
Come to think of it, Lenski had suggested an even better pun for this effect: "Drift Dodger". You'll appreciate that one more after digesting the stuff below. "Survival of the drift dodger". It could work, no?
So let's first talk a little bit about small populations. You remember, of course, that evolution is something that happens in populations. The reason why it cannot happen to a single isolated individual is the essence of one of the three components of the Darwinian Triad: selection. If there is only one organism, then you cannot have differential survival. There are no differences, because there is only one. You cannot win if there is no competition.
If you have two individuals, you could in principle have evolution because there can be differences between the two. Yet, I'm sure I can convince you that it will be extremely difficult for evolution to proceed in this contrived case. The reason for this is that organisms can die. Yes, you read that right: if organisms could not die, then two would be enough to sustain an evolutionary process in principle. But death is inevitable in a finite world with replication, so that settles that. Actually, let me be more precise: death, by itself, does not prevent evolution in small populations. It is instead random death that thwarts evolution, because if death only affected the lower fitness type, then evolution could still work with only two individuals. However, if death strikes randomly, then half the time the fitter one of the pair would be removed, and the one left over then replicates to restore the pair. Because the less-fit individual got to reproduce, the overall population fitness has declined. This is the essence of genetic drift. Now imagine one of the pair is again struck by a mutation. We know that there are far more mutations that reduce fitness than there are those that increase fitness (it is easier to break things by chance than to improve them by random changes). After such a mutation, there is a new lower fitness organisms, and if death strikes randomly, there is again a fifty/fifty chance that the lower fitness organism remains.
You can now understand that, unless beneficial mutations are at least as common as deleterious mutations, this process of a gradual loss of fitness will doom the population. And in the case I just described, this is precisely Muller's ratchet, an inexorable decline in fitness that will doom the small population to extinction. In this extreme example this happened to a population of two, but the process happens anytime the population is extremely small (say, 10 or smaller in most cases).
It turns out that here is a way to resist this decline, but for a population to resist it, it must "live" on a particular type of fitness peak: one with steep slopes. The steeper, the better.
Imagine you have a population that has been dropped into a fitness landscape that has only two peaks: a lower one with steep slopes, and a higher one with gentle slopes (as in the picture below).
A large population will find itself on the blue peak with gentle slopes, because the population that climbed the red peak will be forced into extinction due to the higher fitness of the blue peak. However, if the population size is small, the tables are turned. The small population will not be able to ascend the blue peak, as drift will consistently (and without doubt annoyingly) "throw it back down": mutations with small effect cannot go to fixation when the population size is small. But that intrepid small population can climb the red peak, because it requires big steps to get up there. It might take a while to discover these steps, but once they are found, the population will safely occupy and maintain itself on the the steep peak. This means that this population is robust to drift on such a peak. Were we to transplant the same population to the blue peak it could not maintain itself there, and drift back down that gentle slope. On the red, steep, peak, however, the population is robust to drift. It can dodge the drift. There you have it.
So now we have seen that there are two important exceptions to the "survival of the fittest" rule, the law that stipulates that those genotypes that replicate the fastest should always be the ultimate winners of the competition. This rule holds only at very small mutation rates, and for very large population sizes.
Is there is a more general rule that predicts the winner even at finite mutation rates and small population sizes? A universal law, in a way, that holds without restrictions in mutation rate and population size? I believe that there is such a law indeed, but you'll have to wait for another blog post to find out what it is! That law (I am teasing) is inspired by thermodynamics, which tells us that that small energy (just as high fitness) is not always the winner. That law will set fitness free once and for all.
The research described in this post is based on the paper linked to below. It is openly accessible to everyone.
T. LaBar and C. Adami, "Evolution of drift robustness in small population", Nature Communications 8 (2017) 1012.
But let's get back to the matter at hand. In "Survival-of-the-flattest", organisms that occupy flat (but not terribly high) fitness peaks can outcompete populations that live on high (and very pointy) peaks, but only when the mutation rate is high enough (see schematic drawing in the figure below).

 |
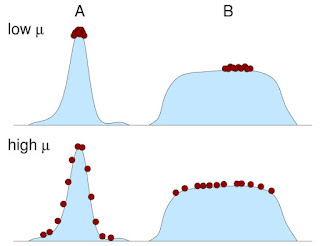| Survival of the flattest. At low mutation rate (top panel), the population living on peak A outcompetes the one living on peak B. At high mutation rate (lower panel), the steepness of peak A implies that many of the mutants on that peak have very low fitness, and the population as a whole will therefore grow poorly. The population on peak B, on the other hand, has mostly neutral mutants, and will outcompete the population at A. (Figure courtesy of Claus Wilke). |
The effect we'll discuss presently concerns population size rather than mutation rate, and just like the "survival-of-the-flattest" effect it violates the semi-edict; the almost-law. We shall call this new effect "survival-of-the-steepest". It goes without saying that this lame attempt at analogizing with the survival-of-the-flattest moniker couldn't be more obvious. But since that original moniker was due to Rich Lenski, and he did not object to this particular use, we'll just run with it and see if it sticks. (It may not.)
Come to think of it, Lenski had suggested an even better pun for this effect: "Drift Dodger". You'll appreciate that one more after digesting the stuff below. "Survival of the drift dodger". It could work, no?
So let's first talk a little bit about small populations. You remember, of course, that evolution is something that happens in populations. The reason why it cannot happen to a single isolated individual is the essence of one of the three components of the Darwinian Triad: selection. If there is only one organism, then you cannot have differential survival. There are no differences, because there is only one. You cannot win if there is no competition.
If you have two individuals, you could in principle have evolution because there can be differences between the two. Yet, I'm sure I can convince you that it will be extremely difficult for evolution to proceed in this contrived case. The reason for this is that organisms can die. Yes, you read that right: if organisms could not die, then two would be enough to sustain an evolutionary process in principle. But death is inevitable in a finite world with replication, so that settles that. Actually, let me be more precise: death, by itself, does not prevent evolution in small populations. It is instead random death that thwarts evolution, because if death only affected the lower fitness type, then evolution could still work with only two individuals. However, if death strikes randomly, then half the time the fitter one of the pair would be removed, and the one left over then replicates to restore the pair. Because the less-fit individual got to reproduce, the overall population fitness has declined. This is the essence of genetic drift. Now imagine one of the pair is again struck by a mutation. We know that there are far more mutations that reduce fitness than there are those that increase fitness (it is easier to break things by chance than to improve them by random changes). After such a mutation, there is a new lower fitness organisms, and if death strikes randomly, there is again a fifty/fifty chance that the lower fitness organism remains.
You can now understand that, unless beneficial mutations are at least as common as deleterious mutations, this process of a gradual loss of fitness will doom the population. And in the case I just described, this is precisely Muller's ratchet, an inexorable decline in fitness that will doom the small population to extinction. In this extreme example this happened to a population of two, but the process happens anytime the population is extremely small (say, 10 or smaller in most cases).
It turns out that here is a way to resist this decline, but for a population to resist it, it must "live" on a particular type of fitness peak: one with steep slopes. The steeper, the better.
Imagine you have a population that has been dropped into a fitness landscape that has only two peaks: a lower one with steep slopes, and a higher one with gentle slopes (as in the picture below).
 |
| A small population will not be able to climb the peek with gentle slopes, because genetic drift will prevent small advances to fix. However, such a population will be able to climb peaks with steep slopes (such as the one on the left) because selection is effective for large advances. |
So now we have seen that there are two important exceptions to the "survival of the fittest" rule, the law that stipulates that those genotypes that replicate the fastest should always be the ultimate winners of the competition. This rule holds only at very small mutation rates, and for very large population sizes.
Is there is a more general rule that predicts the winner even at finite mutation rates and small population sizes? A universal law, in a way, that holds without restrictions in mutation rate and population size? I believe that there is such a law indeed, but you'll have to wait for another blog post to find out what it is! That law (I am teasing) is inspired by thermodynamics, which tells us that that small energy (just as high fitness) is not always the winner. That law will set fitness free once and for all.
The research described in this post is based on the paper linked to below. It is openly accessible to everyone.
T. LaBar and C. Adami, "Evolution of drift robustness in small population", Nature Communications 8 (2017) 1012.
No comments:
Post a Comment